
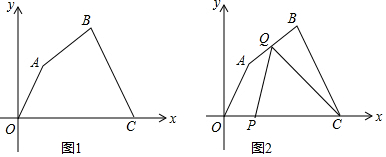
分析 (1)利用待定系数法求AB所在直线的函数表达式;
(2)由题意得:OP=t,PC=14-t,求出PC边上的高为$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$,代入面积公式计算,并根据二次函数的最值公式求出最大值即可;
(3)分别以Q在OA、AB、BC上运动时讨论:
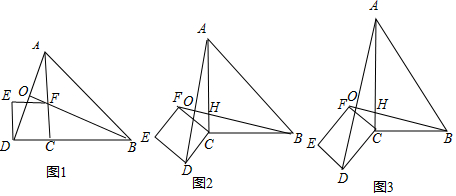
①当0<t≤2时,线段PQ的中垂线经过点C(如图2),
②当2<t≤6时,线段PQ的中垂线经过点A(如图3),
③当6<t≤10时,
i)线段PQ的中垂线经过点C(如图4),
ii)线段PQ的中垂线经过点B(如图5),
只要能画出图形,根据中垂线的性质和勾股定理列方程可得结论.
解答 解:(1)设AB所在直线的函数表达式为y=kx+b,
把A(3,3$\sqrt{3}$)、B(9,5$\sqrt{3}$)代入得:
$\left\{\begin{array}{l}{3k+b=3\sqrt{3}}\\{9k+b=5\sqrt{3}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
∴AB所在直线的函数表达式为y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$;
(2)如图1,由题意得:OP=t,则PC=14-t,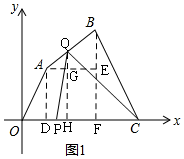
过A作AD⊥x轴于D,过B作BF⊥x轴于F,过Q作QH⊥x轴于H,
过A作AE⊥BF于E,交QH于G,
∵A(3,3$\sqrt{3}$),
∴OD=3,AD=3$\sqrt{3}$,
由勾股定理得:OA=6,
∵B(9,5$\sqrt{3}$),
∴AE=9-3=6,BE=5$\sqrt{3}$-3$\sqrt{3}$=2$\sqrt{3}$,
Rt△AEB中,AB=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$,
tan∠BAE=$\frac{BE}{AE}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠BAE=30°,
点Q过OA的时间:t=$\frac{6}{3}$=2(秒),
∴AQ=$\sqrt{3}$(t-2),
∴QG=$\frac{1}{2}$AQ=$\frac{\sqrt{3}(t-2)}{2}$,
∴QH=$\frac{\sqrt{3}(t-2)}{2}$+3$\sqrt{3}$=$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$,
在△PQC中,PC=14-t,PC边上的高为$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$,t=$\frac{4\sqrt{3}}{\sqrt{3}}$=4(秒),
∴S=$\frac{1}{2}$(14-t)($\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$)=-$\frac{\sqrt{3}}{4}{t}^{2}$+$\frac{5\sqrt{3}}{2}$t+14$\sqrt{3}$(2≤t≤6),
∴当t=5时,S有最大值为$\frac{81\sqrt{3}}{4}$;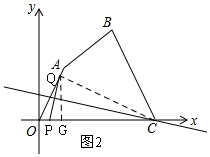
(3)①当0<t≤2时,线段PQ的中垂线经过点C(如图2),
过Q作QG⊥x轴于G,
由题意得:OQ=3t,OP=t,∠AOG=60°,
∴∠OQG=30°,
∴OG=$\frac{3}{2}$t,
∴CG=14-$\frac{3}{2}$t,
sin60°=$\frac{QG}{OQ}$,
∴QG=$\frac{\sqrt{3}}{2}$×3t=$\frac{3\sqrt{3}}{2}$t,
在Rt△QGC中,由勾股定理得:QG2+CG2=QC2=PC2,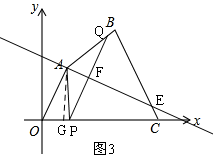
可得方程($\frac{3\sqrt{3}}{2}t$)2+(14-$\frac{3}{2}$t)2=(14-t)2,
解得:t1=$\frac{7}{4}$,t2=0(舍),此时t=$\frac{7}{4}$,
②当2<t≤6时,线段PQ的中垂线经过点A(如图3),
∴AQ=AP,
过A作AG⊥x轴于G,
由题意得:OP=t,AQ=$\sqrt{3}$(t-2),则PG=t-3,AP=$\sqrt{3}$(t-2),
在Rt△AGP中,由勾股定理得:AP2=AG2+PG2,
可得方程:(3$\sqrt{3}$)2+(t-3)2=[$\sqrt{3}$(t-2)]2,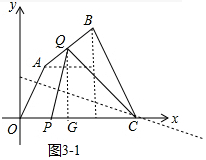
解得:t1=$\frac{3+\sqrt{57}}{2}$,t2=$\frac{3-\sqrt{57}}{2}$(舍去),
此时t=$\frac{3+\sqrt{57}}{2}$;
当PQ的垂直平分线经过点C时,如图3-1中,易知QC=PC=14-t,
QG=$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$,CG=14-$\frac{3}{2}$t,
在Rt△QCG中,(14-t)2=($\frac{\sqrt{3}}{2}$t-2$\sqrt{3}$)2+(14-$\frac{3}{2}$t)2,
整理得t2-4t+6=0,△<0,无解.此种情形不存在.
③当6<t≤10时,
i)线段PQ的中垂线经过点C(如图4),
∴PC=CQ,
由(2)知:OA=6,AB=4$\sqrt{3}$,BC=10,
t=$\frac{6}{3}$+$\frac{4\sqrt{3}}{\sqrt{3}}$=6,
∴BQ=$\frac{5}{2}$(t-6),
∴CQ=BC-BQ=10-$\frac{5}{2}$(t-6)=25-$\frac{5}{2}$t,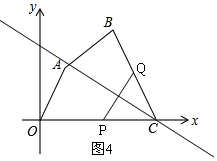
可得方程为:14-t=25-$\frac{5}{2}$t,
解得:t=$\frac{22}{3}$;
ii)线段PQ的中垂线经过点B(如图5),
∴BP=BQ,
过B作BG⊥x轴于G,
则BG=5$\sqrt{3}$,PG=t-9,BQ=$\frac{5}{2}$(t-6),
由勾股定理得:BP2=BG2+PG2,
可得方程为:(5$\sqrt{3}$)2+(t-9)2=[$\frac{5}{2}$(t-6)]2,
解得:t1=$\frac{38+20\sqrt{2}}{7}$,t2=$\frac{38-20\sqrt{2}}{7}$(舍去),
此时t=$\frac{38+20\sqrt{2}}{7}$,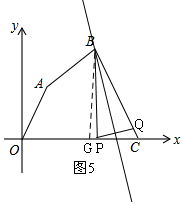
综上所述,t的值为$\frac{7}{4}$或$\frac{3+\sqrt{57}}{2}$或$\frac{22}{3}$或$\frac{38+20\sqrt{2}}{7}$.
点评 本题是四边形的综合题,考查了利用待定系数法求直线的解析式、动点运动问题、组成的三角形的面积问题、二次函数的最值问题、线段垂直平分线的性质以及勾股定理,计算量大,第三问有难度,容易丢解,注意运用数形结合的思想,且第三问主要运用了线段垂直平分线的性质.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
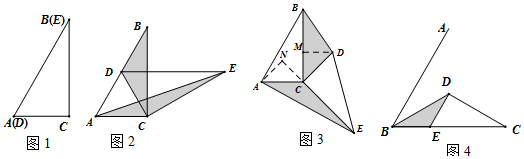
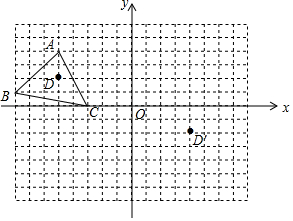 如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,
如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
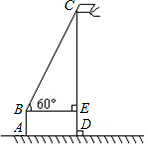 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
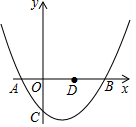 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com