
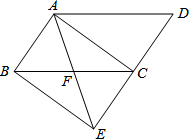
 如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.
如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.分析 (1)由四边形ABCD是平行四边形,得出AB贫血CD,AB=CD,CE=DC,易证得AB=CE,即可得出结论;
(2)由四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∵DC=CE,
∴AB=CE,
∴四边形ABEC是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
∵四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形.
点评 此题考查了平行四边形的性质与判定、矩形的判定、全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆车和一辆货车分别从甲,乙两地相向而行,图中的l1,l2分别表示轿车和货车离甲地的路程s(千米)与行驶时间t(小时)间的关系.
一辆车和一辆货车分别从甲,乙两地相向而行,图中的l1,l2分别表示轿车和货车离甲地的路程s(千米)与行驶时间t(小时)间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
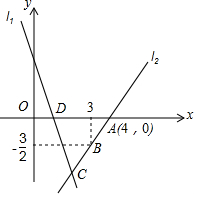 如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.
如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com