
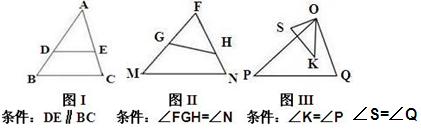
对于两个相似三角形,如果沿周界按对应点顺序环绕方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似。例如:如图①,△ABC∽△A/B/C/,且沿周界ABCA与A/B/C/A/环绕的方向相同,因此△ABC与△A/B/C/互为顺相似;如图②△ABC∽△A/B/C/,且沿周界ABCA与A/B/C/A/环绕的方向相反,因此△ABC与△A/B/C/互为逆相似;

根据图Ⅰ、图Ⅱ、图Ⅲ满足的条件,可分别得下列三对相似三角形:
①△ADE与△ABC;②△FGH与△FNM③△OSK与△OQP.其中,互为顺相似的是 ;互为逆相似的是 。(填写所有符合要求的序号)
(2)如下图在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与A、B、C重合)过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似,画出图形并说明截线满足的条件,不必说明理由。(请至少画出三种截法)

互为顺相似的是 ①②;互为逆相似的是 ③.(2)解答见解析.
【解析】
试题分析:(1)根据互为顺相似和互为逆相似的定义即可作出判断;
(2)根据点P在△ABC边上的位置分为三种情况,需要分类讨论,逐一分析求解.
试题解析:(1)互为顺相似的是 ①②;互为逆相似的是 ③;
(2)根据点P在△ABC边上的位置分为以下三种情况:
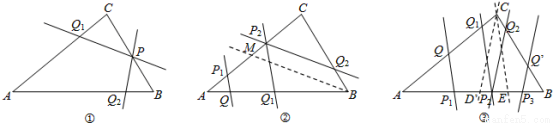
第一种情况:如图①,点P在BC(不含点B、C)上,过点P只能画出2条截线PQ1、PQ2,分别使∠CPQ1=∠A,∠BPQ2=∠A,此时△PQ1C、△PBQ2都与△ABC互为逆相似.
第二种情况:如图②,点P在AC(不含点A、C)上,过点B作∠CBM=∠A,BM交AC于点M.
当点P在AM(不含点M)上时,过点P1只能画出1条截线P1Q,使∠AP1Q=∠ABC,此时△AP1Q与△ABC互为逆相似;
当点P在CM上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ABC,∠CP2Q2=∠ABC,此时△AP2Q1、△Q2P2C都与△ABC互为逆相似.
第三种情况:如图③,点P在AB(不含点A、B)上,过点C作∠BCD=∠A,∠ACE=∠B,CD、CE分别交AB于点D、E.
当点P在AD(不含点D)上时,过点P只能画出1条截线P1Q,使∠AP1Q=∠ACB,此时△AQP1与△ABC互为逆相似;
当点P在DE上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ACB,∠BP2Q2=∠BCA,此时△AQ1P2、△Q2BP2
都与△ABC互为逆相似;
当点P在BE(不含点E)上时,过点P3只能画出1条截线P3Q′,使∠BP3Q′=∠BCA,此时△Q′BP3与△ABC互为逆相似.
考点:相似形综合题.


科目:初中数学 来源:2014-2015学年湖南省郴州市八年级上学期期中考试数学试卷(解析版) 题型:填空题
某红外线遥控器发出的红外线波长为0.000 000 94 m,用科学记数法表示这个数是 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市九年级上期末考试模拟考试数学试卷(解析版) 题型:填空题
从一副扑克牌中取出1张红桃、2张黑桃共3张牌,将这3张牌洗匀后,从中任取1张牌恰好是黑桃的概率是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市九年级上期末考试模拟考试数学试卷(解析版) 题型:选择题
甲、乙两个不透明的口袋中分别装有1个红球、2个黄球和2个红球、4个黄球,把它们分别搅匀,分别从甲、乙两个袋中摸出1个球。现给出下列说法:①从甲袋中摸出红球的概率比从乙袋中摸出红球的概率小;②从甲袋中摸出红球的概率与从乙袋中摸出红球的概率相等;③从甲袋中摸出红球的概率是从乙袋中摸出红球的概率的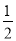 . 其中正确的说法是( )
. 其中正确的说法是( )
A.①② B.② C.②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
便民”水泥代销点销售某种水泥,每吨进价为250元,如果每吨销售价定为290元时,平均每天可售出16吨。
(1)若代销点采取降低促销的方式,试建立每吨的销售利润y(元)与每吨降低x(元)之间的函数关系式。
(2)若每吨售价每降低5元,则平均每天能多售出4吨,问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:填空题
在反比例函数y=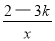 的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。
的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
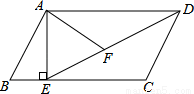
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4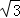 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市八年级上学期期末模拟数学试卷(解析版) 题型:选择题
使分式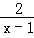 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.x≠1 B.x=1 C.x≤1 D.x≥1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com