
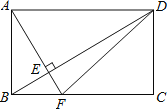
【题目】如图,在长方形ABCD中,AF⊥BD于E,交BC于F,连接DF.
(1)找出图中的一对全等三角形并证明;
(2)直接写出图中所有面积相等但不全等的三角形.
【答案】(1)有,Rt△ABD≌Rt△CDB,理由见解析(答案不惟一);(2)有,△BFD与△BFA,△ABD与△AFD,△ABE与△DFE,△AFD与△BCD面积相等,但不全等.
【解析】试题分析:(1)根据长方形的对边相等,每一个角都是直角可得AB=CD,AD=BC,∠BAD=∠C=90°,然后利用“边角边”证明Rt△ABD和Rt△CDB全等;
(2)根据等底等高的三角形面积相等解答.
试题解析:
(1)有,Rt△ABD≌Rt△CDB,
理由:在长方形ABCD中,AB=CD,AD=BC,∠BAD=∠C=90°,
在Rt△ABD和Rt△CDB中,
 ,
,
∴Rt△ABD≌Rt△CDB(SAS);
(2)有,△BFD与△BFA,△ABD与△AFD,△ABE与△DFE,△AFD与△BCD面积相等,但不全等.


科目:初中数学 来源: 题型:
【题目】近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.现在中国高速铁路营运里程将达到22000公里,将22000用科学记数法表示应为( )
A. 2.2×104 B. 22×103 C. 2.2×103 D. 0.22×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.等弧所对的圆心角相等
B.弧的度数等于该弧所对的圆心角的度数
C.经过三点可以作一个圆
D.三角形的外心到三角形各顶点距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的作直线EF⊥BD分别交AD,BC于E,F两点,连结BE,DF.求证:四边形BFDE为菱形.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:

(1)该班共有多少名学生参加这次测验?
(2)求60.5~70.5这一分数段的频数是多少?
(3)若80分以上为优秀,则该班的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.

(1)求证:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度数;
(3)探究AP、PC、BE之间的数量关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com