
如图,正△ABC中,∠ADE=60°,
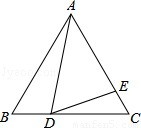
(1)求证:△ABD∽△DCE;
(2)若BD=2,CD=4,求AE的长.
(1)证明见解析;(2)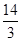 .
.
【解析】
试题分析:(1)在正ABC中,由∠ADE=60°,可知∠ADB+∠EDC=120°,∠BAD+∠ADB=120°,所以∠BAD=∠EDC,又∠B=∠C,可证得△ABD∽△DCE;
(2)由(1)根据相似三角形的对应边成比例,可求得CE的长,从而求出AE的长.
试题解析:(1)在正ABC中,∠B=∠C=60°
∵∠BAD+∠ADB=120°,∠EDC+∠ADB=180°-∠ADE=120°
∴∠BAD=∠EDC
∵∠B=∠C
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,
∴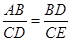
∴
∴AE=AC-CE=6-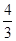 =
=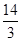
考点:1. 等边三角形的性质;2.相似三角形的判定与性质.


科目:初中数学 来源: 题型:
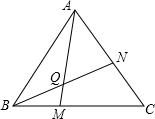
| 正多边形 | 正方形 | 正五边形 | 正六边形 | … | 正n边形 |
| ∠AQN的度数 |
查看答案和解析>>
科目:初中数学 来源: 题型:
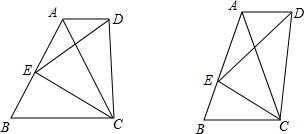 (2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.
(2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
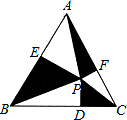 如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=
如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=3
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com