练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x的分式方程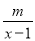+=1的解是非负数，则m的取值范围是（　　）

    A. m＞2 B. m≥2 C. m≥2且m≠3 D. m＞2且m≠3

    C 【解析】试题解析：分式方程去分母得：m-3=x-1， 解得：x=m-2， 由方程的解为非负数，得到m-2≥0，且m-2≠1， 解得：m≥2且m≠3． 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：单选题

    如图，BD、CE分别是△ABC的中线，BD与CE交于点O，则下列结论中正确的是（　　）

    A. B.

    C. D.

    C 【解析】试题分析：∵△ABC的中线BD、CE相交于点O， ∴DE∥BC， ＝， ∴△EOD∽△COB，△AED∽△ABC， ∴＝＝， ＝＝，故A错误； ＝＝，故B错误； ＝，故C正确； ＝＝，故D错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：填空题

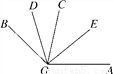
    如图，在∠AOB中，OD是∠BOC的平分线，OE是∠AOC的平分线，若∠AOB＝135°，则∠EOD＝____．

    67.5° 【解析】由图形可知∠DOE=∠DOC+∠EOC，然后根据角平分线的性质，可推出∠DOC=∠BOC，∠EOC=∠AOC，由此可推出∠DOE=∠AOB，最后根据∠AOB的度数，即可求出结论． 【解析】 ∵OD是∠BOC的平分线，OE是∠AOC的平分线， ∴∠DOC=∠BOC，∠EOC=∠AOC， ∴∠DOE=∠DOC+∠EOC=∠AOB， ∵∠AOB=135...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：解答题

    如图,在平面直角坐标系中,A(-1，5)，B（-1，0），C（-4，3）.

    （1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
    （2）写出点A1、B1、C1的坐标；
    （3）在y轴上画出点P，使PA+PC最小；  
    （4）求六边形AA1C1B1BC的面积．.

    （1）作图见解析；（2）A1（1，5）、B1（1，0）、C1（4，3）；（3）见解析；（4）25. 【解析】试题分析：（1）根据题意画出△A1B1C1即可； （2）根据△A1B1C1在坐标系中的位置即可得出各点坐标； （3）连接A1C与y轴交于点P，则P点即为所求； （4）根据S六边形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B即可得出结论． ...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：填空题

    已知4y2+my+1是完全平方式，则常数m的值是_________

    4和-4 【解析】试题解析：∵4y2-my+1是完全平方式， ∴-m=±4，即m=±4． 故答案为：4和-4

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：单选题

    若,则A为(     )

    A. 2ab B. -2ab C. 4ab D. -4ab

    C 【解析】试题解析：∵（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2， ∴A=（a+b）2-（a-b）2=4ab． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    如图，⊙O是△ABC的外接圆，∠ABC=45°，AD是⊙O的切线交BC的延长线于D，AB交OC于E．

    （1）求证：AD∥OC；

    （2）若AE=2，CE=2．求⊙O的半径和线段BE的长．

    （1）证明见解析；（2）． 【解析】 试题分析：（1）连结OA，根据切线的性质得到OA⊥AD，再根据圆周角定理得到∠AOC=2∠ABC=90°，然后根据平行线的判定即可得到结论； （2）设⊙O的半径为R，则OA=R，OE=R-2，AE=2，在Rt△OAE中根据勾股定理可计算出R=4；作OH⊥AB于H，根据垂径定理得AH=BH，再利用面积法计算出OH=，然后根据勾股定理计算出AH=...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：单选题

    如图，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则∠A的度数为（ ）

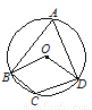
    A. 60° B. 70° C. 120° D. 140°

    A 【解析】试题解析:设 则 解得: 故选A.

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：单选题

    已知m，n是一元二次方程x 2 -4x-3=0的两个实数根，则 为（  ）．

    A. -1 B. -3 C. -5 D. -7

    D 【解析】∵m，n是一元二次方程x²?4x?3=0的两个实数根， ∴m+n=4，mn=?3， ∴(m?2)(n?2)=mn?2(m+n)+4=?3?8+4=?7， 故选D.

    查看答案和解析>>

    同步练习册答案