
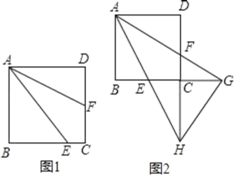
【题目】如图,正方形ABCD中,E为BC边上任意点,AF平分∠EAD,交CD于点F.
(1)如图1,若点F恰好为CD中点,求证:AE=BE+2CE;
(2)在(1)的条件下,求![]() 的值;
的值;
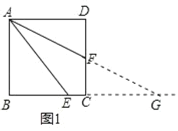
(3)如图2,延长AF交BC的延长线于点G,延长AE交DC的延长线于点H,连接HG,当CG=DF时,求证:HG⊥AG.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)延长BC交AF的延长线于点G,利用“AAS”证△ADF≌△GCF得AD=CG,据此知CG=BC=BE+CE,根据EG=BE+CE+CE=BE+2CE=AE即可得证;
(2)设CE=a,BE=b,则AE=2a+b,AB=a+b,在Rt△ABE中,由AB2+BE2=AE2可得b=3a,据此可得答案;
(3)连接DG,证△ADF≌△DCG得∠CDG=∠DAF,再证△AFH∽△DFG得![]() ,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
解:(1)如图1,延长BC交AF的延长线于点G,
∵AD∥CG,
∴∠DAF=∠G,
又∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠G=∠EAF,
∴EA=EG,
∵点F为CD的中点,
∴CF=DF,
又∵∠DFA=∠CFG,∠FAD=∠G,
∴△ADF≌△GCF(AAS),
∴AD=CG,
∴CG=BC=BE+CE,
∴EG=BE+CE+CE=BE=2CE=AE;
(2)设CE=a,BE=b,则AE=2a+b,AB=a+b,
在Rt△ABE中,AB2+BE2=AE2,即(a+b)2+b2=(2a+b)2,
解得b=3a,b=﹣a(舍),
∴![]() ;
;
(3)如图2,连接DG,
∵CG=DF,DC=DA,∠ADF=∠DCG,
∴△ADF≌△DCG(SAS),
∴∠CDG=∠DAF,
∴∠HAF=∠FDG,
又∵∠AFH=∠DFG,
∴△AFH∽△DFG,
∴![]() ,
,
又∵∠AFD=∠HFG,
∴△ADF∽△HGF,
∴∠ADF=∠FGH,
∵∠ADF=90°,
∴∠FGH=90°,
∴AG⊥GH.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() .
.
(1)当m=3时,求抛物线的顶点坐标;
(2)已知点A(1,2).试说明抛物线总经过点A;
(3)已知点B(0,2),将点B向右平移3个单位长度,得到点C,若抛物线与线段BC只有一个公共点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正比例函数y=k1x与反比例函数y=![]() 的图象相交于A、B两点,AC⊥x轴于点C,CD∥AB交y轴于点D,连接AD、BD,若S△ABD=6,则下列结论正确的是( )
的图象相交于A、B两点,AC⊥x轴于点C,CD∥AB交y轴于点D,连接AD、BD,若S△ABD=6,则下列结论正确的是( )
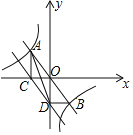
A.k1=﹣6B.k1=﹣3C.k2=﹣6D.k2=﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
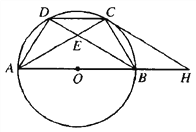
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
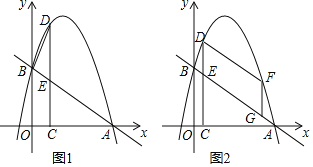
(1)求抛物线的函数表达式
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了回惯顾客,计划于周年店庆当天举行抽奖活动.凡是购物金额达到m元及以上的顾客,都将获得抽奖机会.规则如下:在一个不透明袋子里装有除数字标记外其它完全相同的4个小球,数字标记分别为“a” 、“b”、“c”、“0” (其中正整数a、b、c满足a+b+c=30且a>15).顾客先随机摸出一球后不放回,再摸出第二球,则两球标记的数字之和为该顾客所获奖励金额(单位:元)、经调查发现,每日前来购物的顾客中,购物金额及人数比例如下表所示:
购物金额x (单位:元) | 0<x<100 | 100≤x<200 | 200≤x<300 | x≥300 |
人数比例 |
|
|
|
|
现预计活动当天购物人数将达到200人.
(1)在活动当天,某顾客获得抽奖机会,试用画树状图或列表的方法,求该顾客获得a元奖励金的概率;
(2)以每位抽奖顾客所获奖励金的平均数为决策依据,超市设定奖励总金额不得超过2000元,且尽可能让更多的顾客参与抽奖活动,问m应定为100元?200元?还是300元?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com