
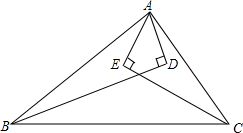
 如图,从△ABC顶点A引∠ABC、∠ACB平分线的垂线,垂足分别为D、E,求证:
如图,从△ABC顶点A引∠ABC、∠ACB平分线的垂线,垂足分别为D、E,求证:分析 (1)分别延长AD、AE与直线BC交于点F、G,根据AD⊥BD,得到∠ADB=∠GDB=90°,再根据BD=BD,∠ABD=∠GBD,证得△ABD≌△GBD,进而得到AD=DG、AE=EF,证得DE∥FG.
(2)根据上题证得AB=BG,AC=CF,由已知图形中的线段数量关系可得FG=BC-BF-CG,BF=BG-EG,CG=CF-FG,从而证得结论.
解答 证明:(1)∵BD平分∠ABC,
∴∠ABD=∠GBD.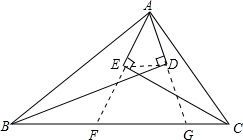
∵在△ABD与△GBD中,
$\left\{\begin{array}{l}{∠ABD=∠GBD}\\{DB=DB}\\{∠ADB=∠GDB=90°}\end{array}\right.$,
∴△ABD≌△GBD(ASA),
∴AD=DG,
∴点D是边AG的中点.
同理,△ACF≌△CEF(ASA),
∴AE=EF,
∴点E是边AF的中点.
∴DE是△AGF的中位线,
∴DE∥GF,
则DE∥BC;
(2)
∵DE是△AGF的中位线,BG=AB,CF=AC,
∴DE=$\frac{1}{2}$FG,
∵FG=BC-BF-CG,BF=BG-EG,CG=CF-FG,
∴DE=$\frac{1}{2}$(AB+AC-BC).
点评 本题考查了三角形的中位线定理及三角形的有关知识,解题的关键是正确的利用中位线定理得到中位线与第三边的位置或数量关系.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
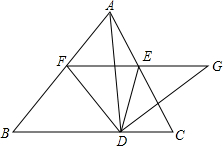 如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.
如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com