
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处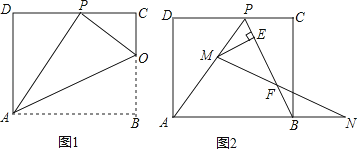
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.
【答案】
(1)
解:如图1
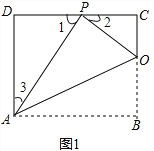 ,
,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴∠1+∠3=90°,
∵由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°,
∴∠2=∠3,
又∵∠D=∠C,
∴△OCP∽△PDA;
∵△OCP与△PDA的面积比为1:4,
∴ ![]() ,
,
∴CP= ![]() AD=4,
AD=4,
设OP=x,则CO=8﹣x,
在Rt△PCO中,∠C=90°,
由勾股定理得 x2=(8﹣x)2+42,
解得:x=5,
∴AB=AP=2OP=10,
∴边CD的长为10;
(2)
解:作MQ∥AN,交PB于点Q,如图2,
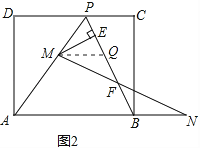
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ= ![]() PQ.
PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
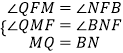 ,
,
∴△MFQ≌△NFB(AAS).
∴QF= ![]() QB,
QB,
∴EF=EQ+QF= ![]() PQ+
PQ+ ![]() QB=
QB= ![]() PB,
PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB= ![]() ,
,
∴EF= ![]() PB=2
PB=2 ![]() ,
,
∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为2 ![]()
【解析】(1)先证出∠C=∠D=90°,再根据∠1+∠3=90°,∠1+∠2=90°,得出∠2=∠3,即可证出△OCP∽△PDA;根据△OCP与△PDA的面积比为1:4,得出CP= ![]() AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42 , 求出x,最后根据AB=2OP即可求出边AB的长;(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=
AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42 , 求出x,最后根据AB=2OP即可求出边AB的长;(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ= ![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF= ![]() QB,再求出EF=
QB,再求出EF= ![]() PB,由(1)中的结论求出PB=
PB,由(1)中的结论求出PB= ![]() ,最后代入EF=
,最后代入EF= ![]() PB即可得出线段EF的长度不变此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等和相似的三角形.
PB即可得出线段EF的长度不变此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等和相似的三角形.


科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )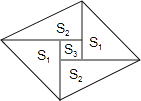
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ![]() ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 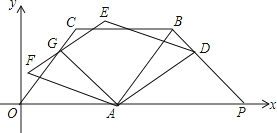
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
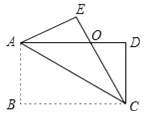
(1)求证:△AOE≌△COD;
(2)若∠OCD=30°,AB=![]() ,求△AOC的面积.
,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初中2000名学生游览“黄河口生态旅游区”,并以此开展“黄河文化”知识竞赛活动,现从中随机抽取若干名学生的得分![]() 满分100分,成绩均为正数
满分100分,成绩均为正数![]() 进行统计,整理出下列竞赛成绩统计表和扇形统计图
进行统计,整理出下列竞赛成绩统计表和扇形统计图![]() 均不完整
均不完整![]() .
.
成绩统计表

如果成绩在90分以上![]() 含90分
含90分![]() 可获得一等奖;70分以上
可获得一等奖;70分以上![]() 含70分
含70分![]() ,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
![]() 本次活动共随机抽取了多少名学生?
本次活动共随机抽取了多少名学生?
![]() 估计本次活动获得二等奖的学生有多少名?
估计本次活动获得二等奖的学生有多少名?
![]() 绘制频数分布直方图.
绘制频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

查看答案和解析>>
科目:初中数学 来源: 题型:
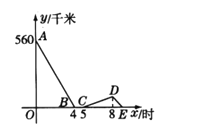
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后停留一段时间,然后分别按原速一同驶往甲地后停车。设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲、乙两地之间的距离为________千米;
(2)求快车和慢车的速度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,车上原有(5a﹣2b)人,中途停车一次,有一些人下车,此时下车的人数比车上原有人数一半还多2人,同时又有一些上车,上车的人数比![]() (7a﹣4b)少3人.
(7a﹣4b)少3人.
(1)用代数式表示中途下车的人数;
(2)用代数式表示中途下车、上车之后,车上现在共有多少人?
(3)当a=10,b=9时,求中途下车、上车之后,车上现在的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的分式方程 ![]() 无解,则m的值为_______.
无解,则m的值为_______.
【答案】-4,-6
【解析】试题分析:去分母得:x(m+2x)-2x(x-3)=2(x-3),
(m+4)x=-6,
当m+4≠0时,
x=![]() ≠0,
≠0,
∵分式方程无解,
∴x-3=![]() -3=0,
-3=0,
解得:m=-6;
当m+4=0即m=-4时,
整式方程无解,分式方程也无解,符合题意,
故m的值为-4或-6.
故答案为:-4或-6.
【题型】填空题
【结束】
19
【题目】计算:
(1)![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com