
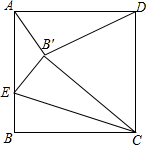
 如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为4-2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$.
如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为4-2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$. 分析 由四边形ABCD是正方形,得到AB=BC=CD=AD,
①当AD=B′D时,如图1,由翻折的性质得,B′C=BC,推出△CDB′是等边三角形,得到∠B′DC=60°,∠ADB′=30°,过B′作B′G⊥AD于G,B′F⊥AB于F,根据勾股定理得到BE=4-2$\sqrt{3}$;②当AB′=B′D时,如图2,则B′在AD的垂直平分线上,推出B′在BC的垂直平分线上,得到BB′=CB′,由翻折的性质得,B′C=BC,推出△BB′C是等边三角形,解直角三角形得到BE=$\frac{\sqrt{3}}{3}$BC=$\frac{2\sqrt{3}}{3}$,③当AB′=AD时,则AB=AB′,推出EC垂直平分BB′,得到A与E重合,B′与D重合,不符合题意,舍去.于是得到结论.
解答 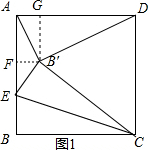 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
①当AD=B′D时,如图1,
由翻折的性质得,B′C=BC,
∴B′D=B′C=CD,
∴△CDB′是等边三角形,
∴∠B′DC=60°,
∴∠ADB′=30°,
过B′作B′G⊥AD于G,B′F⊥AB于F,
∴AF=B′G=$\frac{1}{2}$×2=1,DG=$\sqrt{3}$,
∴AG=FB′=2-$\sqrt{3}$,
∵BE=B′E,EF=1-BE,
∴(2-$\sqrt{3}$)2+(1-BE)2=BE2,
∴BE=4-2$\sqrt{3}$;
②当AB′=B′D时,如图2,
则B′在AD的垂直平分线上,
∴B′在BC的垂直平分线上,
∴BB′=CB′,
由翻折的性质得,B′C=BC,
∴△BB′C是等边三角形,
∴∠BCE=30°,
∴BE=$\frac{\sqrt{3}}{3}$BC=$\frac{2\sqrt{3}}{3}$,
③当AB′=AD时,则AB=AB′,
∵EB=EB′,CB=CB′,
∴点E、C在BB′的垂直平分线上,
∴EC垂直平分BB′,
∴A与E重合,
∴B′与D重合,不符合题意,舍去.
综上所述,BE的长为4-2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$.
故答案为:4-2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$.
点评 本题考查了翻折变换,翻折的性质,勾股定理,等腰三角形的判定,熟练掌握翻折的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是14.
如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是14.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com