
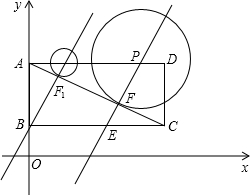
 ��P�˶�����P1λ��ʱ��ֱ��Lǡ�þ�����B����ʱֱ�ߵĽ���ʽ��y=2x+1
��P�˶�����P1λ��ʱ��ֱ��Lǡ�þ�����B����ʱֱ�ߵĽ���ʽ��y=2x+1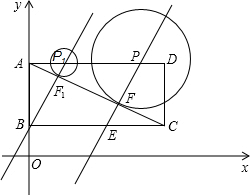
 =
=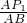 ��AP1=
��AP1=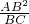 =
=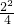 =1��
=1��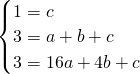 ��
��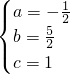 ��
�� x2+
x2+ x+1��
x+1�� ��
�� -1��
-1�� x2+
x2+ x+1��
x+1�� ��
�� ����ʱ��AP=
����ʱ��AP= -r��AP=
-r��AP=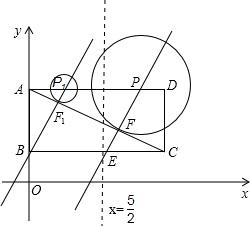
 +r��
+r�� =��
=�� -1����2��
-1����2�� ��
�� -rʱ��
-rʱ�� -r=5-
-r=5- �����r=
�����r= -
- ���������⣬��ȥ����
���������⣬��ȥ���� +rʱ��
+rʱ�� +r=5-
+r=5- �����r=
�����r= -
- ��
�� -
- ��
�� ��
�� ��
�� ��AP��4��
��AP��4��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 |
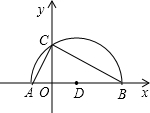 BC=4
BC=4| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
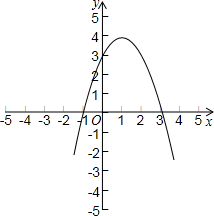 ��B�����е�B�ڵ�A���Ҳ࣬������ͼ����y�ύ�ڵ�C���Ҿ�����D��2��3����
��B�����е�B�ڵ�A���Ҳ࣬������ͼ����y�ύ�ڵ�C���Ҿ�����D��2��3����| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����ͼ��ƽ��ֱ������ϵxOy�У�ֱ��AB�ֱ���x��y�ύ�ڵ�B��A���뷴����������ͼ��ֱ��ڵ�C��D��CE��x���ڵ�E��OA=3��OB=6��OE=2��
��֪����ͼ��ƽ��ֱ������ϵxOy�У�ֱ��AB�ֱ���x��y�ύ�ڵ�B��A���뷴����������ͼ��ֱ��ڵ�C��D��CE��x���ڵ�E��OA=3��OB=6��OE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
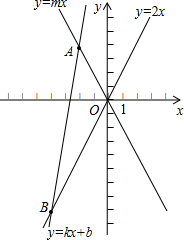 ��֪����ͼ��ƽ��ֱ������ϵxOy�У�ֱ��y=kx+b��k��0����ֱ��y=mx��m��0�����ڵ�A��-2��4����
��֪����ͼ��ƽ��ֱ������ϵxOy�У�ֱ��y=kx+b��k��0����ֱ��y=mx��m��0�����ڵ�A��-2��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
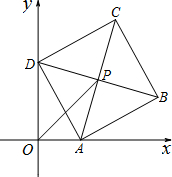 ��֪����ͼ��ƽ��ֱ������ϵxOy�У�������ABCD�ı߳�Ϊ4�����Ķ���A��x������������˶�������D��y������������˶�����A��D������ԭ���غϣ�������B��C���ڵ�һ���ޣ��ҶԽ���AC��BD�ཻ�ڵ�P������OP��
��֪����ͼ��ƽ��ֱ������ϵxOy�У�������ABCD�ı߳�Ϊ4�����Ķ���A��x������������˶�������D��y������������˶�����A��D������ԭ���غϣ�������B��C���ڵ�һ���ޣ��ҶԽ���AC��BD�ཻ�ڵ�P������OP��| 2 |
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com