
(7分)如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,
0),与反比例函数y= 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(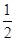 ,n).连结OB,若S△AOB=1.
,n).连结OB,若S△AOB=1.
(1)求反比例函数与一次函数的关系式;

科目:初中数学 来源: 题型:
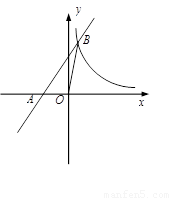
(本题12分)如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙G交x轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙G的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形.那么,直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形,如果存在,请直接写出所有符合题意的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分8分)如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A在y轴上,点C在x轴上,且![]() ,OB=OC.
,OB=OC.
(1)求点B的坐标;
(2)点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H,设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PM∥CB交线段AB于点M,过点M作MR⊥OC,垂足为R,线段MR分别交直线PH、OB于点E、G,点F为线段PM的中点,联结EF.
①判断EF与PM的位置关系;
②当t为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分12分)
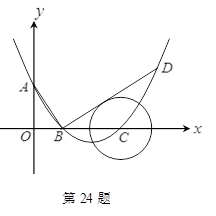
如图,在平面直角坐标系中,顶点为(,
)的抛物线交
轴于
点,交
轴于
,
两点(点
在点
的左侧), 已知
点坐标为(
,
)。
(1)求此抛物线的解析式;
(2)过点作线段
的垂线交抛物线于点
, 如果以点
为圆心的圆与直线
相切,请判断抛物线的对称轴
与⊙
有怎样的位置关系,并给出证明;
 (3)已知点
(3)已知点是抛物线上的一个动点,且位于
,
两点之间,问:当点
运动到什么位置时,
的面积最大?并求出此时
点的坐标和
的最大面积.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(辽宁大连卷)数学 题型:解答题
(11·大连)(本题11分)如图,在平面直角坐标系中,点A、B、C的坐标分别
为(0,2)、(-1,0)、(4,0).P是线段OC上的一动点(点P与点O、C不重合),过点P
的直线x=t与AC相交于点Q .设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
.设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
部分的面积为S.
(1)点B关于直线x=t的对称点B′的坐标为________;
(2)求S与t的函数关系式.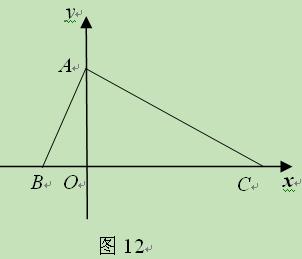
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省盐城地区九年级上学期期末考试数学卷 题型:解答题
. (本题满分12分)
如图,在平面直角坐标系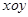 中,点
中,点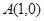 ,点
,点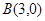 ,点
,点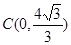 ,直线经过点
,直线经过点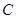 ,
,

1.(1)若在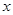 轴上
轴上 方直线
方直线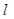 上存在点
上存在点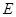 使△
使△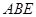 为等边三角形,求直线
为等边三角形,求直线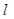 所表达的函数关系式;
所表达的函数关系式;
2.(2)若在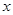 轴上方直线上有且只有
轴上方直线上有且只有 三个点能和
三个点能和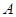 、
、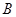 构成直角三角形,求直线
构成直角三角形,求直线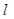 所表达的函数关系式;
所表达的函数关系式;
3.(3)若在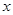 轴上方直线上有且只有一个点在函数
轴上方直线上有且只有一个点在函数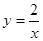 的图形上,求直线
的图形上,求直线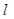 所表达的函数关系式.
所表达的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com