
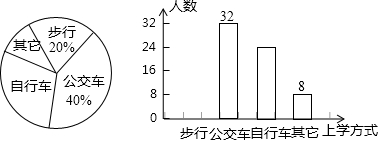
分析 (1)根据公交车所占比例为40%,而由条形图知一共有32人坐公交车上学,从而求出总人数;
(2)由扇形统计图知:步行占20%,而由(1)总人数已知,从而求出步行人数,补全条形图;
(3)根据被调查的总人数及骑自行车上学的人数,用样本中骑自行车人数所占比例乘以总人数1200,与的400个自行车停车位比较即可得答案.
解答 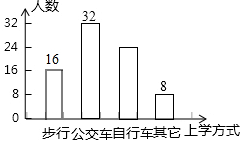 解:(1)32÷40%=80,
解:(1)32÷40%=80,
故答案为:80;
(2)“步行”的人数为:80×20%=16(人),
补全图,如下:
(3)∵骑自行车上学的人有80-(16+32+8)=24(人),
∴$\frac{24}{80}$×1200=360,
∵360<400,
∴够用.
点评 此题考查了条形统计图和扇形统计图及用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )
如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )| A. | 2,(-22017,22017×$\sqrt{3}$) | B. | 2,(-22018,0) | ||
| C. | $\sqrt{3}$,(-22017,22017×$\sqrt{3}$) | D. | $\sqrt{3}$,(-22018,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com