
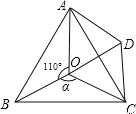
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
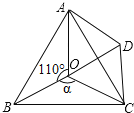
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
【答案】(1)证明见解析;(2)当α=150°时,△AOD是直角三角形,理由见解析;(3)当α的度数为125°或110°或140°时,△AOD是等腰三角形.
【解析】试题分析:(1)根据旋转的性质可得出![]() ,结合题意即可证得结论;
,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
试题解析:(1)证明:∵将△BOC绕点C按顺时针方向旋转![]() 得△ADC,
得△ADC,
∴CO=CD,∠OCD=![]() ,
,
∴△COD是等边三角形,
(2)当![]() 时,△AOD是直角三角形.
时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60![]() 得△ADC,
得△ADC,
∴△BOC≌△ADC,
![]()
又∵△COD是等边三角形,
∴∠ODC=![]() ,
,
![]()
![]()
![]()
∴△AOD不是等腰直角三角形,即△AOD是直角三角形。
(3)①要使AO=AD,需∠AOD=∠ADO,
![]()
![]()
![]()
②要使OA=OD,需∠OAD=∠ADO.
![]()
![]()
![]()
③要使OD=AD,需∠OAD=∠AOD.
![]()
![]()
![]()
解得![]()
综上所述:当α的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形。
时,△AOD是等腰三角形。


科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
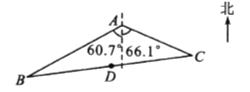
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() m,
m, ![]() m,点
m,点![]() 位于点
位于点![]() 的南偏西60. 7°方向,点
的南偏西60. 7°方向,点![]() 位于点
位于点![]() 的南偏东66. 1°方向.
的南偏东66. 1°方向.
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0. 1 m,参考数据:
间的距离.(结果精确到0. 1 m,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6。P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足为M、N设AP=x。

(1)在△ABC中,AB= ;
(2)当x= 时,矩形PMCN的周长是14;
(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断,并加以说明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:![]()
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com