
【题目】已知a、b分别对应数轴上A、B两点,并且满足|a﹣2|+(3a+2b)2=0,点P为数轴上一个动点,它对应的数是x
(1)填空:a= ,b= ,AB= ;
(2)若P为线段AB上一点,并且PA=3PB,求x的值;
(3)若P点从A点出发以每秒2个单位的速度运动,那么出发几秒钟后,线段PA=4PB?
![]()
【答案】(1)2;﹣3;5;(2)![]() ;(3)2秒或
;(3)2秒或![]() 秒.
秒.
【解析】
(1)根据平方与绝对值的和为0,可得平方与绝对值同时为0,可得a、b的值,根据两点间的距离,可得答案;
(2)根据两点间的距离公式,可得答案;
(3)设点P运动了t秒,根据两点间的距离公式,可得答案.
解:(1)∵![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴AB=2﹣(﹣3)=5.
故答案为:2;﹣3;5.
(2)根据题意得:2﹣x=3[x﹣(﹣3)],
解得:x=﹣![]() .
.
答:x的值为﹣![]() .
.
(3)∵点A在点B的右边,
∴若想PA=4PB,则点P从点A向左运动.
设点P运动的时间为t秒,则点P对应的数是2﹣2t,
根据题意得:2t=4×|2﹣2t﹣(﹣3)|,
解得:t1=2,t2=![]() .
.
答:出发2秒钟或![]() 秒钟后,线段PA=4PB.
秒钟后,线段PA=4PB.


科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )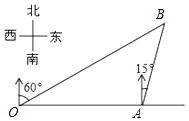
A.3 ![]() km
km
B.3 ![]() km
km
C.4 km
D.(3 ![]() ﹣3)km
﹣3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
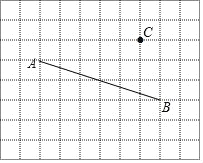
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( ) 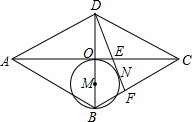
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
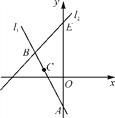
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨![]() 元收费
元收费![]() 如果超过20吨,未超过的部分按每吨
如果超过20吨,未超过的部分按每吨![]() 元收费,超过的部分按每吨
元收费,超过的部分按每吨![]() 元收费
元收费![]() 设某户每月用水量为x吨,应收水费为y元.
设某户每月用水量为x吨,应收水费为y元.
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 若该城市某户5月份水费平均为每吨
若该城市某户5月份水费平均为每吨![]() 元,求该户5月份用水多少吨?
元,求该户5月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com