Question

1．已知：在Rt△ABC中，∠ABC=90°，∠C=60°，现将一个足够大的直角三角形的顶点P放在斜边AC上．
（1）设三角板的两直角边分别交边AB，BC于点M，N．
①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；
②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．
（2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB，BC于点M，N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB，BC的延长线于点M，N．
①请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；
②在①的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是1cm或5cm．

Answer 1

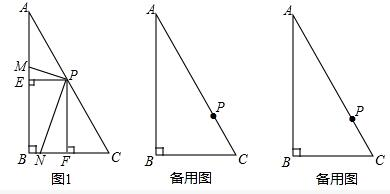
分析 （1）①求出∠AEP=∠B=∠PFC=90°，∠APE=∠C=60°，根据AAS推出两三角形全等即可；②根据已知条件得到AB=$\sqrt{3}$BC，求出PE=$\frac{1}{2}$BC，PF=$\frac{1}{2}$AB，根据相似三角形的判定推出△PFN∽△PEM，根据相似三角形的性质得到$\frac{PM}{PN}$=$\frac{PE}{PF}$=$\frac{1}{\sqrt{3}}$，即可得出答案．
（2）①根据相似三角形的性质得到$\frac{AP}{PC}=\frac{PE}{PF}$=2，设CF=x，则PE=2x，求出PF=$\sqrt{3}$x，根据相似三角形的性质即可得到结论；②求出CP=2cm，分为两种情况：第一种情况：当N在线段BC上时，得出△PCN是等边三角形，求出CN=CP=2cm，即可得到结论；第二种情况：当N在线段BC的延长线上时，求出CN=PC=2cm，即可得到结论．

解答 （1）解：①△AEP≌△PFC，
理由是：∵P为AC中点，
∴AP=PC，
∵PE⊥AB，PF⊥BC，∠B=90°，
∴∠AEP=∠B=∠PFC=90°，
∴PF∥AB，PE∥BC，
∴∠APE=∠C=60°，
在△AEP和△PFC中
$\left\{\begin{array}{l}{∠APE=∠C}\\{∠AEP=∠PFC}\\{AP=PC}\end{array}\right.$
∴△AEP≌△PFC（AAS）；

②△PFN∽△PEM，PN=$\sqrt{3}$PM，
理由是：∵在Rt△ACB中，∠ABC=90°，∠C=60°，
∴AB=$\sqrt{3}$BC，
∵PE∥BC，PF∥AB，P为AC中点，
∴E为AB中点，F为BC中点，
∴PE=$\frac{1}{2}$BC，PF=$\frac{1}{2}$AB，
∴$\frac{PE}{PF}=\frac{BC}{AB}$=$\frac{1}{\sqrt{3}}$，
∵∠PEB=∠B=∠PFB=90°，
∴∠EPF=90°，
∵∠MPN=90°，
∴∠EPM=∠NPF=90°-∠MPF，
∵∠PEM=∠PFN=90°，
∴△PFN∽△PEM，
∴$\frac{PM}{PN}$=$\frac{PE}{PF}$=$\frac{1}{\sqrt{3}}$，
∴PN=$\sqrt{3}$PM．
（2）①PM=2PN，如图1，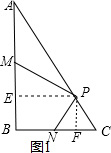
证明：过P作PE⊥AB于E，PF⊥BC于F，
∵∠AEP=∠PFC=∠B=90°，
∴PE∥BC，
∴∠APE=∠C，
∴△AEP∽∠PFC，
∴$\frac{AP}{PC}=\frac{PE}{PF}=\frac{2PC}{PC}$=2，
设CF=x，则PE=2x，
在Rt△PFC中，∠C=60°，∠PFC=90°，
∴PF=$\sqrt{3}$x，
∵在四边形BFPE中，∠BFP=∠B=∠BEP=90°，
∴∠EPF=90°，
即∠EPM+∠MPF=90°，
∵∠NPF+∠MPF=90°，
∴∠NPF=∠EPM，
∵∠MEP=∠PFN=90°，
∴△PEM∽△PFN，
∴$\frac{PM}{PN}=\frac{PE}{PF}$=$\frac{2\sqrt{3}}{3}$，
∴PM=$\frac{2\sqrt{3}}{3}$PN；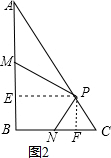

②解：∵在Rt△ABC中，∠B=90°，∠C=60°，BC=3cm，
∴AC=2BC=6cm，
∵AP=2PC，
∴CP=2cm，
分为两种情况：第一种情况：当N在线段BC上时，如图2，
∵△PCN是等腰三角形，∠C=60°，CP=2cm，
∴△PCN是等边三角形，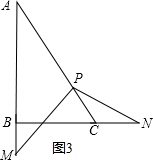
∴CN=CP=2cm，
∴BN=BC-CN=3cm-2cm=1cm；
第二种情况：当N在线段BC的延长线上时，如图3，
∵∠PCN=180°-60°=120°，
∴要△PCN是等腰三角形，只能PC=CN，
即CN=PC=2cm，
∴BN=BC+CN=3cm+2cm=5cm，
即BN的长是1cm或5cm，
故答案为：1cm或5cm．

点评 本题考查了等边三角形性质和判定，等腰三角形性质和判定，三角形中位线，相似三角形的性质和判定的应用，题目综合性比较强，有一定的难度．用了分类讨论思想．