
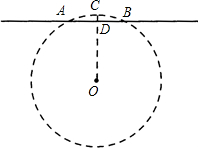
 今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).
今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).分析 先根据垂径定理求出AD的长,然后在Rt△AOD中,运用勾股定理将圆的半径求出,进而可求出直径CE的长.
解答 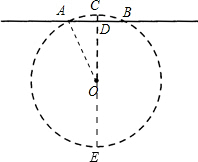 解:本题用现在的数学语言表述是:“如图所示,CE为⊙O的直径,CE⊥AB,垂足为D,CD=1寸,AB=1尺,求直径CE长是多少寸?”
解:本题用现在的数学语言表述是:“如图所示,CE为⊙O的直径,CE⊥AB,垂足为D,CD=1寸,AB=1尺,求直径CE长是多少寸?”
设直径CE的长为2x寸,则半径OC=x寸.
∵CE为⊙O的直径,弦AB⊥CE于D,AB=10寸,
∴AD=BD=$\frac{1}{2}$AB=5寸,
连接OA,则OA=x寸,
根据勾股定理得x2=52+(x-1)2,
解得x=13,
CE=2x=2×13=26(寸).
故所求直径为26寸.
点评 此题是一道古代问题,考查了垂径定理和勾股定理的应用.通过此题,可知我国古代的数学已发展到很高的水平.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 (1)有理数a,b在数轴上位置如图所示,求-|a|+|b|;
(1)有理数a,b在数轴上位置如图所示,求-|a|+|b|;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
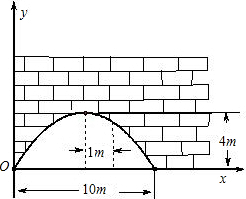 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
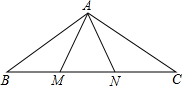 如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )
如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )| A. | 120° | B. | 70° | C. | 60° | D. | 50°. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com