
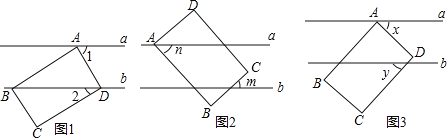
����Ŀ����ͼ����֪a��b��������ABCD�ĵ�A��ֱ��a�ϣ�B��C��D������ƽ�����ƶ��仯����������״��Сʼ�ձ��ֲ��䣩������������������
��1��ͼ1������B��D��ֱ��b�ϣ���C��ֱ��b���·�����2=30�������1=������
��2��ͼ2������D��ֱ��a���Ϸ�����C��ƽ��ֱ��a��b�ڣ���B��ֱ��b���·���m��n��ʾ�ǵĶ�������д��m��n��������ϵ��˵�����ɣ�
��3��ͼ3������D��ƽ��ֱ��a��b�ڣ���B��C��ֱ��b���·���x��y��ʾ�ǵĶ�����x��y�����������ϵʽx2��2xy+y2=100����x�Ķ�����
���𰸡���1��60�㣻��2��90�㣻��3��50��
����������1�����ȸ��ݽǵĺͲ��ϵ�������ADB�Ķ������ٸ���ƽ���ߵ����ʿɵá�1�Ķ�������2����C��EF��a,����a��b�ɵ�EF��a��b, �ٸ���ƽ���ߵ����ʿɵá�4+m=��BCD��n=��4�����õ��������ɵô𰸣���3����D��c��b,���������ɵ�x-y=10,�ٸ���ƽ���ߵ����ʿɵ�x+y=90������������Ͽɵô𰸣�
�⣺��1�����ı���ABCD�dz����Σ�
���ADC=90�㣬
�ߡ�2=30�㣬
���ADB=60�㣬
��a��b��
���1=��ADB=60�㣬
�ʴ�Ϊ��60�㣻
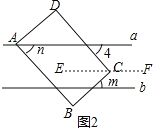
��2����ͼ2����C��EF��a��
��AB��CD��
��n=��4��
��a��b��
��EF��a��b��
���4+m=��BCD=90�㣬
��m+n=90�㣻
��3����ͼ3����D��c��b��
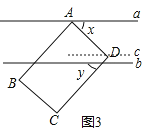
��a��b��
��a��b��c��
��x2��2xy+y2=100��
�ࣨx��y��2=100��
��x��y��
��x��y=��10����ȥ����
��x��y=10����
��a��b��
��a��b��c��
�ߡ�ADC=90�㣬
��x+y=90����
��+�ڵã�x=50�㣮
���㾦�����⿼�����ı����ۺϣ��Լ�ƽ���ߵ����ʺ��ж����ؼ���������ֱ��ƽ�У��ڴ�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ƽ���ı��������ĶԽ��ߵĽ�����ת90�����ܹ����������غϣ�����ı�����( )
A. ���� B. ���� C. ������ D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ���֯���꼶ʦ��ȥ��ɽ���б�ҵ��������������꼶�鳤����ʦ��С����С��ͬѧ�й������ĶԻ���
����ʦ����ƽ�����˹�˾��60����45�������ͺŵĿͳ��ɹ����ã�60���ͳ�ÿ��ÿ�������45���Ĺ�200Ԫ����
С����������ѧУ���꼶ʦ��������������˹�˾����4��60����2��45���Ŀͳ�����ɽ�ιۣ�һ������5000Ԫ����
С���������Ǿ��꼶ʦ������5��60����1��45���Ŀͳ�������������
�������϶Ի�������������⣺
��1��ƽ�����˹�˾60����45���Ŀͳ�ÿ��ÿ������ֱ��Ƕ���Ԫ��
��2����С�����������������꼶ʦ�����ù�˾�һ�죬����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽƬ��4�ű߳�Ϊa��ֹ���Σ�3�ű߳�Ϊb�������� (a<b)��8�ſ�Ϊa����Ϊb�ij����Σ�����15��ֽƬ����ƴ��һ�������Σ���ô�ó����εij�Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤����һ���������в��������������Ƕ۽ǡ�
��֪����ABC
��֤����A����B����C�в������������Ƕ۽�
֤�������裮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽس�������ǰ�����20km���ҵأ�һ��ʱ���С�����ҵس�����ͬһ��·����ǰ���أ�С������2.5h���ھ��ҵ�7.5km����С��������֮������ͬʱ�����յ㣮ͼ���߶�AB��CD�ֱ��ʾС����С�����ҵصľ���y��km����С������ʱ��x��h���Ĺ�ϵ��
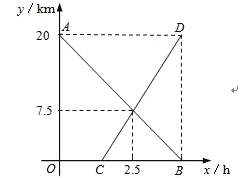
��1�����߶�AB��CD����ʾ��y��x֮��ĺ�������ʽ��
��2��С�������ʱ����������16km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ʵ������һ���������Ұڶ����ڶ�������ѡȡ������˲ʱ״̬����C�����E��F����ĸ��Ƿֱ�Ϊ��ACE=������BCF=�£���ʱ��F����ڵ�E������acm����ð���CD�ij��ȣ����ú�a�������µ�ʽ�ӱ�ʾ��
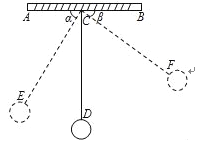
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB=4��BC=3��������ֱ��l���������½ǵĶ���B������ת90����ͼ��λ�ã��������½ǵĶ������������ת90����ͼ��λ�������Դ����ƣ�����������ת2017�κ���A��������ת��������������·��֮����_________��
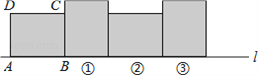
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com