
 如图所示,有一抛物线形门洞,地面宽度为8m,有一宽6m,高4m的车刚好能通过这个门洞,求这个门洞的高度.(精确到0.01m)
如图所示,有一抛物线形门洞,地面宽度为8m,有一宽6m,高4m的车刚好能通过这个门洞,求这个门洞的高度.(精确到0.01m) 分析 由题意可知各点的坐标,A(-4,0),B(4,0),D(-3,4),又由抛物线的顶点在y轴上,即可设抛物线的解析式为y=ax2+c,然后利用待定系数法即可求得此二次函数的解析式,继而求得这个门洞的高度.
解答 解:建立如图所示的平面直角坐标系.
由题意可知各点的坐标,A(-4,0),B(4,0),D(-3,4).
设抛物线的解析式为:y=ax2+c(a≠0),把B(4,0),D(-3,4)代入,得
$\left\{\begin{array}{l}{16a+c=0}\\{9a+c=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{4}{7}}\\{b=\frac{64}{7}}\end{array}\right.$,
∴该抛物线的解析式为:y=-$\frac{4}{7}$x2+$\frac{64}{7}$,
则C(0,$\frac{64}{7}$).
∵$\frac{64}{7}$m≈9.1m.
答:门洞的高度是9.1m.
点评 此题考查了二次函数在实际生活中的应用.题目难度适中,解此题的关键是理解题意,求得相应的函数解析式,注意待定系数法的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
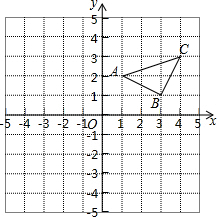 作图题(不写作法)已知:如图,在平面直角坐标系中.
作图题(不写作法)已知:如图,在平面直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
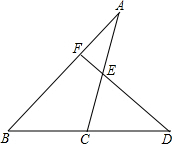 如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.
如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
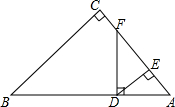 如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
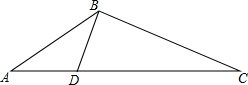 在△ABC中,D是边BC上一点,且∠ABD=∠C.
在△ABC中,D是边BC上一点,且∠ABD=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com