
分析 (1)利用平方差公式以及完全平方公式分解因式得出即可;
(2)首先利用完全平方公式去括号,进而利用拆项与补项法进而重新分解因式得出即可;
(3)首先补项2x2(1-y2)进而利用完全平方公式以及平方差公式分解因式进而得出答案;
(4)利用提取公因式法分解因式得出即可;
(5)直接利用十字相乘法分解因式得出即可.
解答 解:(1)x4-2(a2+b2)x2+(a2-b2)2;
=x4-2(a2+b2)x2+(a2+b2)2-4a2b2
=[x2-(a2+b2)]2-(2ab)2
=[(x2-(a-b)2][(x2-(a+b)2]
=(x+a-b)(x-a+b)(x+a+b)(x-a-b);
(2)(ax+by+ay)2+(bx-ay)(ax+by+ay)+(bx-ay)2
=(ax+by)2+2(ax+by)ay+(ay)2+(bx-ay)(ax+by)+(bx-ay)ay+(bx-ay)2
=[(ax+by)2+(bx-ay)2]+{(ax+by)[2ay+(bx-ay)]}+(ay)[(bx-ay)+ay]
=(x2+y2)(a2+b2)+(ax+by)(bx+ay)+bxay
=(x2+y2)(a2+b2)+abx2+aby2+xya2+xyb2+abxy
=(x2+y2)(a2+b2)+ab(x2+y2)+xy(a2+b2+ab)
=(x2+y2)(a2+b2+ab)+xy(a2+b2+ab)
=(x2+y2+xy)(a2+b2+ab);
(3)(1+y)2-2x2(1+y2)+x4(1-y)2
=(1+y)2+2x2(1-y2)+x4(1-y2)-2x2(1-y2)-2x2(1+y2)
=[1+y+x2(1-y)]2-2x2(1-y2+1+y2)
=(x2-x2y+y+1)2-4x2
=(x2-x2y+y+1+2x)(x2-x2y+y+1-2x)
=[(x2+2x+1)-y(x2-1)][(x2-2x+1)-y(x2-1)]
=[(x+1)2-y(x2-1)][(x-1)2-y(x2-1)]
=(x+1)(x+1-xy+y)(x-1)(x-1-xy-y);
(4)abcx2+(a2b2+c2)x+abc
=abx•cx+abx•ab+cx•c+ab•c
=(abx+c)(cx+ab);
(5)(a-b)x2+2ax+a+b
=[(a-b)x+a+b](x+1)
=(ax-bx+a+b )(x+1).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.


科目:初中数学 来源: 题型:解答题
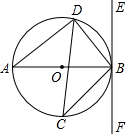 如图,⊙O的直径AB的长为10,弦BD的长为6,点C为$\widehat{AB}$上的一点,过点B的切线EF,连接AD,CD,CB;
如图,⊙O的直径AB的长为10,弦BD的长为6,点C为$\widehat{AB}$上的一点,过点B的切线EF,连接AD,CD,CB;查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c=asinA | B. | c=$\frac{a}{sinA}$ | C. | a=btanA | D. | c=$\frac{a}{cosA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com