分析:(1)根据方程的特点,移项后,再进行因式分解,将方程化为x(x-1)=0的形式,然后解得方程的解.
(2)方程的左边是一个完全平方式,可以因式分解为(x-2)2的形式,因此,此方程可用因式分解法解答.
(3)根据方程特点,应用配方法解答.
解答:解:(1)因式分解法
移项得,3x
2-x=0,
因式分解,得x(x-1)=0,
∴x=0或x-1=0,
∴x
1=0,x
2=1.
(2)因式分解法
因式分解得,(x-2)
2=0,
所以x-2=0,
∴x
1=x
2=2.
(3)配方法
移项得,m
2-2m=1,
配方得,m
2-2m+1=2,
即(m-1)
2=2,
∴m-1=
或m-1=
-,
∴
m=1+或m=1-.
点评:本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后,方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的式子的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法时,即可考虑用求根公式法或配方法,这两种方法适用于任何一元二次方程.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案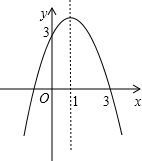 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: