
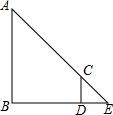
 如图所示,在四边形ABCD中.AB=AD,∠BAD=∠C=90°,BC=5,CD=3,过点A作AE⊥BC,垂足为点E,请你利用旋转变换求AE的长.
如图所示,在四边形ABCD中.AB=AD,∠BAD=∠C=90°,BC=5,CD=3,过点A作AE⊥BC,垂足为点E,请你利用旋转变换求AE的长. 分析 过点A作AF⊥CD交CD延长线于F,可以证明△ABE≌△ADF,即可证明四边形AECF是正方形,据此即可求解.
解答  解:过点A作AF⊥CD交CD延长线于F,
解:过点A作AF⊥CD交CD延长线于F,
∵AE⊥BC,AF⊥CD,∠C=90,
∴四边形AECF是矩形.
∴∠EAF=90,∠AEB=∠AFC=90,
∴∠EAD+∠DAF=90.
∵∠BAD=90,
∴∠EAD+∠BAE=90,
∴∠DAF=∠BAE.
∴在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠AFC=∠AEB}\\{∠BAE=∠FAD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF (AAS).
∴AF=AE,BE=DF,
∴正方形AECF.
∴AE=CE=CF,
∴BE=BC-CE=BC-AE=5-AE,DF=CF-CD=AE-CD=AE-3,
∴5-AE=AE-3,
∴AE=4.
点评 本题考查了全等三角形的判定与性质,正确作出辅助线,证明△ABE≌△ADF是解决本题的关键.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来:
如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.| 所批发土豆的数量x(千克) | 70 | 90 | 100 |
| 每月所得毛利润W(元) | 420 | 540 | 570 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.
如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高.
古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com