
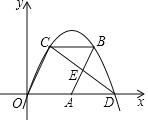
【题目】如图,点A为x轴上一点,点B的坐标为(a,b),以OA,AB为边构造OABC,过点O,C,B的抛物线与x轴交于点D,连结CD,交边AB于点E,若AE=BE,则点C的横坐标为( )
A.a﹣bB.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图①,抛物线y=a(x2+2x-3)(a≠0)与x轴交于点A和点B,与y轴交于点C,且OC=OB.
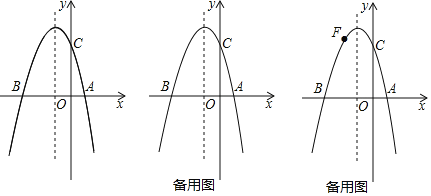
(1)直接写出点B的坐标是( , ),并求抛物线的解析式;
(2)设点D是抛物线的顶点,抛物线的对称轴是直线l,连接BD,线段OC上的点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;
(3)若点F为抛物线第二象限图象上的一个动点,连接BF,CF,当△BCF的面积是△ABC面积的一半时,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
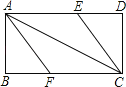
(1)求证:四边形AFCE是菱形;
(2)若AE=13cm,△ABF的周长为30cm,求△ABF的面积;
(3)在线段AC上是否存在一点P,使得2AE2=ACAP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
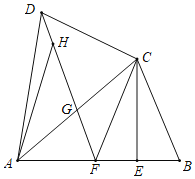
【题目】已知四边形ABCD中,AB=AD,AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,△DGC∽△ADC.
(1)求证:CD=CF;
(2)H为线段DG上一点,连结AH,若∠ADC=2∠HAG,AD=5,DC=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与![]() 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线![]() ,并写出当
,并写出当![]() 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
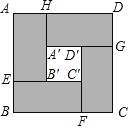
【题目】创客联盟的队员想用3D打印完成一幅边长为4米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形A′B′C′D′,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如下表
材料 | 甲 | 乙 |
价格(元/米2) | 60 | 30 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
(1)A′D′的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于3时,预备材料的购买资金700元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
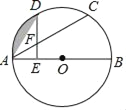
【题目】如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a≠0)的对称轴为直线x=﹣1.
(1)b= ;(用含a的代数式表示)
(2)当a=﹣1时,若关于x的方程ax2+bx+c=0在﹣4<x<1的范围内有解,求c的取值范围;
(3)若抛物线过点(﹣1,﹣1),当0≤x≤1时,抛物线上的点到x轴距离的最大值为4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+(2m+1)x+m=0有两个实数根.
(1)求m的取值范围
(2)是否存在实数m,使方程的两实数根的倒数和为0?若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com