
科目:初中数学 来源: 题型:
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点 为N(0,6),且与x轴交于A、B两点.
为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
解分式方程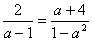 (在表格中的下划线处填空)
(在表格中的下划线处填空)
| 解题过程 | 解题依据(用文字或符号填写知识的名称或具体内容,每空一个) |
| 解: | 此外不填 |
| 两边同乘以 ________________① | 示例(以下三个依据形式任选其一均可) 等式的基本性质 等式两边同乘以一 若 |
| 解这个方程得: | _ |
| 检验:把a的值代入方程 左边=_____=右边④ |
_________________________________________________⑤ |
| 所以_______________⑥ | 此外不填 |

查看答案和解析>>
科目:初中数学 来源: 题型:
⑴证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;
要求:根据图1写出定理的已 知、求证、证明;在证明过程中,至少有两外写
知、求证、证明;在证明过程中,至少有两外写 出推理的依据(“已知”除外)
出推理的依据(“已知”除外)
⑵如图2,在□ABCD中,对角线交点为O,A1、B1、C1、D1分别是OA、OB、OC、OD的中点,A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点,…以此类推
 若在□ABCD的周长为1,直接用算式表示各四边形的周长之
若在□ABCD的周长为1,直接用算式表示各四边形的周长之 和l;
和l;
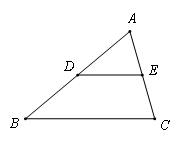 ⑶借助图形3反映的规律,猜猜l可能是多少?
⑶借助图形3反映的规律,猜猜l可能是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A. k>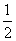 B. k≥
B. k≥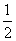 C. k>
C. k>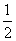
 且k≠1 D. k≥
且k≠1 D. k≥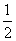 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
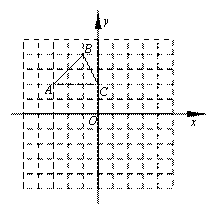
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(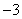 ,2),B(
,2),B( ,4),C(0,2).
,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(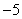 ,
,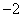 ),画出平移后的△A2B2C2;
),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com