
【题目】已知,抛物线y=ax2+2ax+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)当a>0时,如图所示,若点D是第三象限方抛物线上的动点,设点D的横坐标为m,三角形ADC的面积为S,求出S与m的函数关系式,并直接写出自变量m的取值范围;请问当m为何值时,S有最大值?最大值是多少.

【答案】(1) y=﹣x2﹣2x+3或y=x2+2x﹣3;(2) S=﹣![]() (m2+3m)(﹣3<m<0);当m=﹣
(m2+3m)(﹣3<m<0);当m=﹣![]() 时,S取最大值,最大值为
时,S取最大值,最大值为![]() .
.
【解析】
(1)根据点B的坐标及OC=3OB可得出点C的坐标,再根据点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)过点D作DE⊥x轴,交AC于点E,利用二次函数图象上点的坐标特征可求出点A、C的坐标,进而即可得出线段AC所在直线的解析式,由点D的横坐标可找出点D、E的坐标,再利用三角形的面积公式即可得出S与m的函数关系式,利用配方法可找出S的最大值.
(1)∵点B的坐标为(1,0),OC=3OB,
∴点C的坐标为(0,3)或(0,﹣3),
将点B(1,0)、C(0,3)或(0,﹣3)代入y=ax2+2ax+c,
![]() 或
或![]()
解得:![]() 或
或![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+3或y=x2+2x﹣3.
(2)过点D作DE⊥x轴,交AC于点E,如图所示.
∵a>0,
∴抛物线的解析式为y=x2+2x﹣3,
∴点C的坐标为(0,﹣3).
当y=0时,有x2+2x﹣3=0,
解得:x1=﹣3,x2=1,
∴点A的坐标为(﹣3,0),
利用待定系数法可求出线段AC所在直线的解析式为y=﹣x﹣3.
∵点D的横坐标为m,
∴点D的坐标为(m,m2+2m﹣3),点E的坐标为(m,﹣m﹣3),
∴DE=﹣m﹣3﹣(m2+2m﹣3)=﹣m2﹣3m,
∴S=![]() DE×|﹣3﹣0|=﹣
DE×|﹣3﹣0|=﹣![]() (m2+3m)(﹣3<m<0).
(m2+3m)(﹣3<m<0).
∵﹣![]() <0,且S=﹣
<0,且S=﹣![]() (m2+3m)=﹣
(m2+3m)=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∴当m=﹣![]() 时,S取最大值,最大值为
时,S取最大值,最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】在由6个大小相同的小正方形组成的方格中:
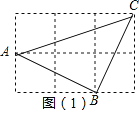
(1)如图(1),△ABC 的三个顶点A、B、C都在格点上,试判断△ABC的形状,并加以证明;
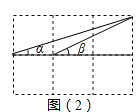
(2)如图(2),连结三格和两格的对角线,利用(1)的图形特征,求出∠α+∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,

(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:CE=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武胜县白坪—飞龙乡村旅游度假村橙海阳光景点组织![]() 辆汽车装运完
辆汽车装运完![]() 三种脐橙共
三种脐橙共![]() 吨到外地销售.按计划,
吨到外地销售.按计划,![]() 辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
脐橙品种 |
|
|
|
每辆汽车运载量(吨) |
|
|
|
每吨脐橙获得(元) |
|
|
|
![]() 设装运
设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如果装运每种脐橙的车辆数都不少于
如果装运每种脐橙的车辆数都不少于![]() 辆,那么车辆的安排方案有几种?
辆,那么车辆的安排方案有几种?
![]() 设销售利润为
设销售利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com