
 ��ͼ����ƽ��ֱ������ϵ�У�������ABC���������㶼�������η���ĸ����
��ͼ����ƽ��ֱ������ϵ�У�������ABC���������㶼�������η���ĸ�������� ��1������ͼ��д�������������꼴�ɣ�
��2����������д��A�䡢B�䡢C�����꣬�ٻ���ͼ�μ����ж�
��3����������д��A�塢B�塢C�����꣬�ٻ���ͼ�μ����жϣ�
��� �⣺��1��A��3��4����B��1��2����C��5��1����
��2�������겻�䣬�����궼����-1��
�ɵã�A�䣨3��-4����B�䣨1��-2����C�䣨5��-1����
��A��B��C����ͼ��ʾ
��A��B��C�����ABC����x��Գƣ� 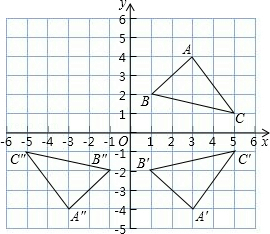
��3�������궼���䣬�����궼����-1��
�ɵã�A�壨-3��-4����B�壨-1��-2����C�壨-5��-1����
��A��B��C����ͼ��ʾ��
��A��B��C�����ABC����ԭ��Գƣ�
���� ���⿼����ͼ��λ�Ʊ任����Գƣ�ԭ��ԳƵ�֪ʶ������Ĺؼ����������⣬��ȷ����ͼ�Σ������п��������ͣ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������������У�ÿ��С�����εı߳���Ϊ1����ABC�����������λ����ͼ��ʾ������ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮
��ͼ���������������У�ÿ��С�����εı߳���Ϊ1����ABC�����������λ����ͼ��ʾ������ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽��ҹ�����ˮ���Ƿ��ܵ��ձ��˷�����Ⱦ | |
| B�� | �˽����ǰ�50��ͬѧ�ϴ��¿���ѧ�ɼ� | |
| C�� | �˽�һ�����ܵ��ݵ�ʹ������ | |
| D�� | �˽�һ���ҹ����������ĺ˵�ͷ��ɱ�˰뾶 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com