
【题目】如图,将等边△ABC绕点C顺时针旋转120得到 ![]() EDC,连接AD,BD.
EDC,连接AD,BD.
则下列结论:
①AC=AD;
②BD ![]() AC;
AC;
③四边形ACED是菱形.
其中正确的个数是( )
A.O
B.1
C.2
D.3
【答案】D
【解析】解 ;∵等边△ABC绕点C顺时针旋转120°得到△EDC,
∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,
∴∠ACD=120°-60°=60°.
∴△ACD是等边三角形.
∴AC=AD,AC=AD=DE=CE. 故①符合题意;
∴四边形ACED是菱形,故③符合题意;
∵等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,
∴AB=BC=CD=AD.
∴四边形ABCD是菱形,
∴BD⊥AC,故②符合题意
故应选 :D.
根据旋转的性质,旋转前后的对应边和对应角相等,结合等边三角形的判定,即可得到△ACD是等边三角形,从而判断①的正误;
然后依据菱形的判定定理,四条边均相等的四边形为菱形,即可判断③的正误.再根据菱形的性质对角线互相垂直即可判断出②正确。


科目:初中数学 来源: 题型:
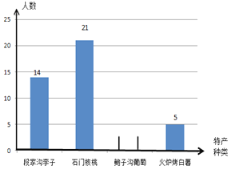
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“我最喜爱的卢龙特产”调查活动.
调查问卷
在下面四种卢龙特产中,你最喜爱的是( )(单选)
A.段家沟李子 B.石门核桃
C.鲍子沟葡萄 D.火炉烤白薯
将调查问卷整理后绘制成如图所示的不完整条形统计图:
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“段家沟李子”的同学有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.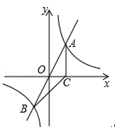
(1)求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距50千米,某日下午甲、乙两人分别骑自行车和骑摩托车从A地出发驶往B地如图所示,图中的折线PQR和线段MN分别表示甲、乙两人所行驶的路程S(千米)与该日下午时间t(时)之间的关系.请根据图象解答下列问题:
(1)直接写出:甲骑自行车出发 小时后,乙骑摩托车才开始出发;乙骑摩托车比甲骑自行车提前 小时先到达B地;
(2)求出乙骑摩托车的行驶速度;甲骑自行车在下午2时至5时的行驶速度;
(3)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
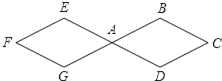
A. 点F B. 点E C. 点A D. 点C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com