
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=![]() .
.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度;
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
【答案】(1)![]() (2)存在,F点的坐标为(2,-3)(3)
(2)存在,F点的坐标为(2,-3)(3)![]() 或
或![]() (4)
(4)![]() ,
,![]()
【解析】解:(1)方法一:由已知得:C(0,-3),A(-1,0)
将A、B、C三点的坐标代入得 ………………… 2分
………………… 2分
解得:
所以这个二次函数的表达式为:![]() ………………… 3分
………………… 3分
方法二:由已知得:C(0,-3),A(-1,0)
设该表达式为:![]() ………………… 2分
………………… 2分
将C点的坐标代入得:![]()
所以这个二次函数的表达式为:![]() …………………3分
…………………3分
(注:表达式的最终结果用三种形式中的任一种都不扣分)
(2)方法一:存在,F点的坐标为(2,-3)
理由:易得D(1,-4),所以直线CD的解析式为:![]()
∴E点的坐标为(-3,0)
由A、C、E、F四点的坐标得:AE=CF=2,AE∥CF
∴以A、C、E、F为顶点的四边形为平行四边形
∴存在点F,坐标为(2,-3) ………………… 6分
方法二:易得D(1,-4),所以直线CD的解析式为:![]()
∴E点的坐标为(-3,0)
∵以A、C、E、F为顶点的四边形为平行四边形
∴F点的坐标为(2,-3)或(―2,―3)或(-4,3)
代入抛物线的表达式检验,只有(2,-3)符合
∴存在点F,坐标为(2,-3) ………………… 6分
(3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
代入抛物线的表达式,解得![]() …………………8分
…………………8分
②当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,-r),
代入抛物线的表达式,解得![]() ………………… 9分
………………… 9分
∴圆的半径为![]() 或
或![]() .
.
(4)过点P作y轴的平行线与AG交于点Q,

易得G(2,-3),直线AG为![]() .
.
设P(x,![]() ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ![]() .
.
![]()
当![]() 时,△APG的面积最大
时,△APG的面积最大
此时P点的坐标为![]() ,
,![]() . ………………… 12分
. ………………… 12分
(1)根据已知条件,易求得C、A的坐标,可用待定系数法求出抛物线的解析式;
(2)根据以点A、C、E、F为顶点的四边形为平行四边形,由平行四边形的性质以及二次函数的性质得出AE=CF,AE∥CF即可得出答案.
(3)分两种情况进行讨论:①当直线MN在x轴上方时;②当直线MN在x轴下方时,设圆的半径,代入抛物线求解
(4)易求得AC的长,由于AC长为定值,当P到直线AG的距离最大时,△APG的面积最大.可过P作y轴的平行线,交AG于Q;设出P点坐标,根据直线AG的解析式可求出Q点坐标,也就求出PQ的长,进而可得出关于△APG的面积与P点坐标的函数关系式,根据函数的性质可求出△APG的最大面积及P点的坐标,根据此时△APG的面积和AG的长,即可求出P到直线AC的最大距离.


科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校要求需要完成总面积为80m2的三项任务,它们的面积比例及每人每分钟完成各项目的工作量如下图所示:
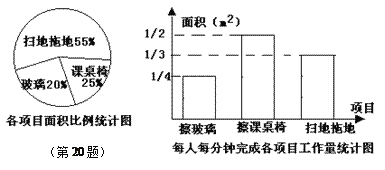
(1)从上述统计图中可知:每人每分钟给擦课桌椅、擦玻璃、扫地拖地的面积分别
是 m2, m2, m2;
(2)如果x人每分钟擦玻璃的面积是ym2,那么y关于x的函数关系式是 ;
(3)他们一起完成扫地和拖地的任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅.如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某土建工程共需动用15台挖运机械,每台机械每分钟能挖土3 m3或者运土2 m3.为了使挖土和运土工作同时结束,安排了x台机械运土,这里x应满足的方程是( )
A.2x=3(15-x)
B.3x-2x=15
C.15-2x=3x
D.3x=2(15-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织“我的中国梦”演讲比赛,每位选手的最后得分为去掉一个最低分、一个最高分后的平均数.7位评委给小红同学的打分是:9.3,9.6,9.4,9.8,9.5,9.1,9.7,则小红同学的最后得分是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=![]() ,PA=4.
,PA=4.
(1)求证:△ABP≌△ACF;
(2)求证:AC2=PAAE;
(3)求PB和PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形的三个内角的度数分别为40°,60°,80°,则这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,

在![]() 中,
中,![]() °,若点
°,若点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]() .
.
灵活应用:如图2,![]() 中,
中,![]() °,
°,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,

将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的长:
的长:
(2)判断![]() 的形状:
的形状:
(3)请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2,C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com