
 已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.
已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$. 分析 根据图形关于y轴的对称特点,找出相应的点,把相应的点连接起来即可;分别求出各点的坐标,利用梯形的性质求解.
解答 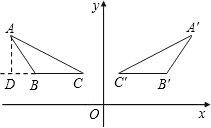 解:如图所示,过A点作AD⊥BC,交CB的延长线于点D,
解:如图所示,过A点作AD⊥BC,交CB的延长线于点D,
则∠ABD=180°-∠ABC=180°-120°=60°.
在Rt△ABD中,BD=AB•cos∠ABD=2×$\frac{1}{2}$=1,
AD=AB•sin∠ABD=2×$\frac{\sqrt{3}}{2}$又知点B的坐标为(-3,1),
∴点A的坐标为(-4,1+$\sqrt{3}$).
∵AA′⊥y轴,BB′⊥y轴,
∴AA′⊥BB′,
∵AB与A′B′不平行,
∴以点A,B,B′,A′为顶点的四边形是等腰梯形.
由点A,B的坐标可求得AA′=2×4=8,BB′=2×3=6,
∴梯形ABB′A′的面积=$\frac{1}{2}$(AA′+BB′)•AD=$\frac{1}{2}$×(8+6)×$\sqrt{3}$=7$\sqrt{3}$.
故答案是:7$\sqrt{3}$.
点评 本题考查了轴对称的性质:1、对称轴是一条直线;2、垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等;3、在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等;4、在轴对称图形中,对称轴把图形分成完全相等的两份;5、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:| 甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
| 乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,AB=4,BC=8,点E,F分别在BC,CD边上,且∠EAF=∠ABC=60°.
如图,?ABCD中,AB=4,BC=8,点E,F分别在BC,CD边上,且∠EAF=∠ABC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点.若点E,F分别是AB,AC上的点,且∠EDF=90°,下列结论中正确结论的个数是( )
如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点.若点E,F分别是AB,AC上的点,且∠EDF=90°,下列结论中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
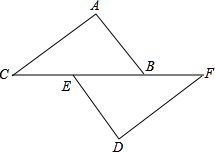 如图,已知点B,E,C,F在一条直线上,BF=CE,AC=DF,现要使△ABC与△DEF全等,需要添加的一个条件是∠ACB=∠DFE或AB=DE.
如图,已知点B,E,C,F在一条直线上,BF=CE,AC=DF,现要使△ABC与△DEF全等,需要添加的一个条件是∠ACB=∠DFE或AB=DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$或$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com