
分析 (1)易证△AOB是等腰直角三角形,两直线之间的距离是1,则过B作l1的垂线,垂线段长是1,利用勾股定理求得BD的长,即可求得D的坐标,同理求得E的坐标;
(2)求出O到直线的距离,据此即可作出判断;
(3)首选求得到原点距离是1和3时直线对应的b的值,则b的范围即可求得.
解答 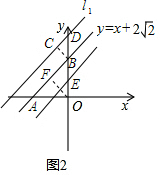 解:(1)如图,y=x+2$\sqrt{2}$中令x=0时y=2$\sqrt{2}$,则B的坐标是(0,2$\sqrt{2}$),
解:(1)如图,y=x+2$\sqrt{2}$中令x=0时y=2$\sqrt{2}$,则B的坐标是(0,2$\sqrt{2}$),
令y=0,0=x+2$\sqrt{2}$,解得:x=-2$\sqrt{2}$,则A的坐标是(-2$\sqrt{2}$,0).
则OA=OB=2$\sqrt{2}$,即△ABC是等腰直角三角形,
过B作BC⊥l1于点C,则BC=1.
则△BCD是等腰直角三角形,BC=CD=1,
则BD=$\sqrt{2}$,即D的坐标是(0,3$\sqrt{2}$),
同理,E的坐标是(0,$\sqrt{2}$).
则与y轴交点的坐标为(0,$\sqrt{2}$)和(0,3$\sqrt{2}$);
(2)在等腰直角△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2.
过O作OF⊥AB于点F.
则OF=$\frac{1}{2}$AB=1.
当0<r<1时,0个;
当r=1时,1个; 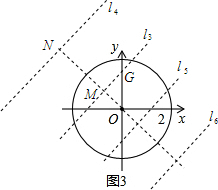
当1<r<3时,2个;
当 r=3时,3个;
当3<r时,4个.
(3)OM是第二、四象限的角平分线,
当OM=2-1=1时,则l3与y轴的交点G,G的坐标是(0,$\sqrt{2}$),即b=$\sqrt{2}$,
同理当ON=3时,b=3$\sqrt{2}$,
当直线在原点O下方时,b=-$\sqrt{2}$和b=-3$\sqrt{2}$.
则当-3$\sqrt{2}$<b<-$\sqrt{2}$或$\sqrt{2}$<b<3$\sqrt{2}$时,2为半径的圆上只有两个点到直线y=x+b的距离为1.
故答案是:-3$\sqrt{2}$<b<-$\sqrt{2}$或$\sqrt{2}$<b<3$\sqrt{2}$.
点评 本题是圆与一次函数的综合题,考查了直线和圆的位置关系,正确理解直线y=x+2$\sqrt{2}$与x、y轴的交点以及原点构成等腰直角三角形是关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
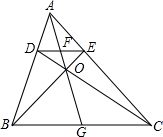 如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明:
如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为3,点E在边AB上,AE=1,点Q是边AD上的动点,过点Q作QH⊥BC于H,在BC上H点左侧取点P,使得PH=1,若设BP=x,EQ2=y.
如图,正方形ABCD的边长为3,点E在边AB上,AE=1,点Q是边AD上的动点,过点Q作QH⊥BC于H,在BC上H点左侧取点P,使得PH=1,若设BP=x,EQ2=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com