
分析 (1)根据已知提供的信息,把代数式的分子分母同时乘以$\sqrt{7}-\sqrt{6}$即可;
(2)把代数式的分子分母同时乘以$\sqrt{n+1}-\sqrt{n}$即可;
(3)根据(2)中规律进行变形化简即可.
解答 (1)$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})×(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}-\sqrt{6}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})×(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$;
(3)($\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{5}+2}$+…+$\frac{1}{\sqrt{2010}+\sqrt{2009}}$+$\frac{1}{\sqrt{2011}+\sqrt{2010}}$)(1+$\sqrt{2011}$)
=($\sqrt{2}$-1+$\sqrt{3}-\sqrt{2}$+…+$\sqrt{2010}$-$\sqrt{2009}$+$\sqrt{2011}-\sqrt{2010}$)×(1+$\sqrt{2011}$)
=($\sqrt{2011}-1$)×(1+$\sqrt{2011}$)
=2011-1
=2010.
点评 此题主要考查二次根式的化简方法-------分母有理化的探索与运用,分析阅读材料中的解题思路,灵活进行模仿运用是解题的关键.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:选择题
| A. | 两个图形对应点连线的垂直平分线是它们的对称轴 | |
| B. | 经过线段中点的直线是它的对称轴 | |
| C. | 角平分线是角的对称轴 | |
| D. | 对称轴是两个对称点连线的垂直平分线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
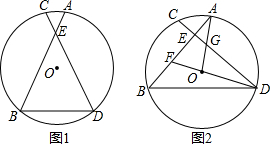
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -21 | B. | 21 | C. | -24 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com