
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF= ![]() AB.
AB.
(3)如图3,若∠EDF的两边分别交AB,AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE,AB,CF之间的数量关系.
【答案】
(1)
解:如图1中,

∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4,
∵点D是线段BC的中点,
∴BD=DC= ![]() BC=2,
BC=2,
∵DF⊥AC,即∠CFD=90°,
∴∠CDF=30°,
又∵∠EDF=120°,
∴∠EDB=30°,
∴∠BED=90°
∴BE= ![]() BD=1
BD=1
(2)
解:如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.

∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD= ![]() AB
AB
(3)
解:结论不成立.结论:BE﹣CF= ![]() AB.
AB.

∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD= ![]() AB
AB
【解析】(1)如图1中,只要证明∠BED=90°,根据直角三角形30度角性质即可解决问题.(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.只要证明△BDM≌△CDN,△EDM≌△FDN即可解决问题.(3)(2)中的结论不成立.结论:BE﹣CF= ![]() AB,证明方法类似(2).
AB,证明方法类似(2).
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:
(甲)①作∠A的角平分线L.
②以B为圆心,BC长为半径画弧,交L于D点,则D即为所求.
(乙)①过B作平行AC的直线L.
②过C作平行AB的直线M,交L于D点,则D即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )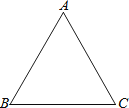
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
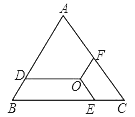
A. 3 B. 6 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示: 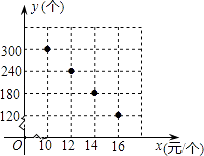
(1)y与x之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(单位:元)与销售单价x (单位:元/个)之间的函数关系式;
(3)在(2)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,
∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,结果保留整数).
≈1.732,结果保留整数). 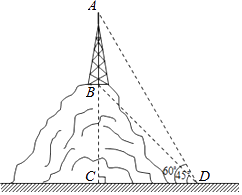
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3) 
(1)求此二次函数的解析式和顶点坐标;
(2)直线y2=kx+b过B、C两点,请直接写出当y1>y2时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com