
【题目】如图,在![]() 中,
中,![]() 在
在![]() 边上,
边上,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于
于![]() ,则
,则![]() ______.
______.
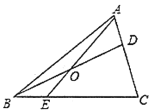
【答案】![]()
【解析】
过O作BC的平行线交AC与G,由中位线的知识可得出AD:DC=1:2,根据已知和平行线分线段成比例得出AD=DG=GC,AG:GC=2:1,AO:OE=2:1,再由同高不同底的三角形中底与三角形面积的关系可求出BE:EC的比.
解:如图,过O作OG∥BC,交AC于G,
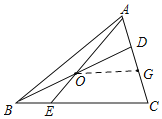
∵O是BD的中点,
∴G是DC的中点.
又AD:DC=1:2,
∴AD=DG=GC,
∴AG:GC=2:1,AO:OE=2:1,
∴S△AOB:S△BOE=2
设S△BOE=S,S△AOB=2S,又BO=OD,
∴S△AOD=2S,S△ABD=4S,
∵AD:DC=1:2,
∴S△BDC=2S△ABD=8S,S四边形CDOE=7S,
∴S△AEC=9S,S△ABE=3S,
∴ =
=![]() =
=![]()


科目:初中数学 来源: 题型:
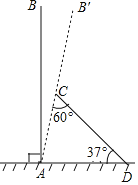
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
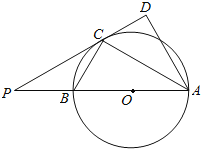
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB.延长DC交AB的延长线于点P.
(1)求证:PC2=PAPB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=900,且EF交正方形外角的平分线CF于点F
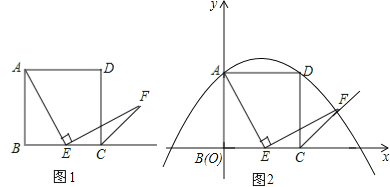
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线![]() 上,求此时点F的坐标.
上,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题,如图1,在等边![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,若
,若![]() ,试求
,试求![]() 的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
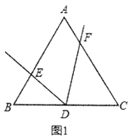
(1)注意到![]() 为等边三角形,且
为等边三角形,且![]() ,可得
,可得![]() ,于是可证
,于是可证![]() ,进而可得
,进而可得![]() ,注意到
,注意到![]() 为
为![]() 中点,
中点,![]() ,因此
,因此![]() 和
和![]() 满足的等量关系为______.
满足的等量关系为______.
(2)设![]() ,
,![]() ,则
,则![]() 的取值范围是______.结合(1)中的关系求
的取值范围是______.结合(1)中的关系求![]() 与
与![]() 的函数关系.
的函数关系.
(3)在平面直角坐标系![]() 中,根据已有的经验画出
中,根据已有的经验画出![]() 与
与![]() 的函数图象,请在图2中完成画图.
的函数图象,请在图2中完成画图.
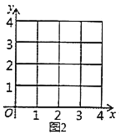
(4)回到原问题,要使![]() ,即为
,即为![]() ,利用(3)中的图象,通过测量,可以得到原问题的近似解为
,利用(3)中的图象,通过测量,可以得到原问题的近似解为![]() ______(精确到0.1)
______(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?

查看答案和解析>>
科目:初中数学 来源: 题型:
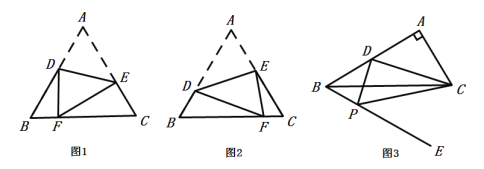
【题目】(1)如图1,△ABC为等边三角形,点D、E分别为边AB、AC上的一点,将图形沿线段DE所在的直线翻折,使点A落在BC边上的点F处求证:![]() ;
;
(2)如图2,按图1的翻折方式,若等边△ABC的边长为4,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图3,在![]() 中,
中,![]() ,点D是AB边上的中点,在BC的下方作射线BE,使得
,点D是AB边上的中点,在BC的下方作射线BE,使得![]() ,点P是射线BE上一个动点,当
,点P是射线BE上一个动点,当![]() ,求BP的长.
,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分別与⊙O交于点D,E,则下列说法一定正确的是( )
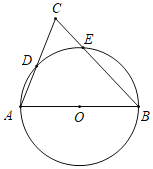
A.连接BD,可知BD是△ABC的中线B.连接AE,可知AE是△ABC的高线
C.连接DE,可知![]() D.连接DE,可知S△CDE:S△ABC=DE:AB
D.连接DE,可知S△CDE:S△ABC=DE:AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com