
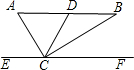
 如图,在Rt△ABC中,DC是斜边AB上的中线,EP过点C且平行于AB.若∠BCF=35°,求∠ACD的度数.
如图,在Rt△ABC中,DC是斜边AB上的中线,EP过点C且平行于AB.若∠BCF=35°,求∠ACD的度数.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | -2≤x≤2 | B. | x≥-2且x≠1 | C. | x>-2 | D. | -2≤x≤2且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
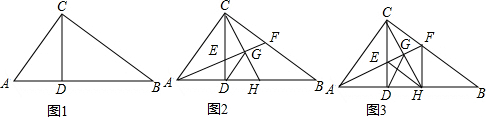
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
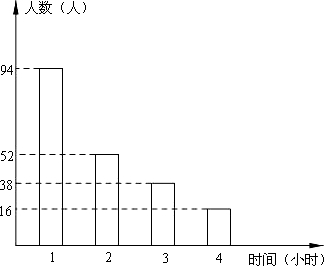 某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市次项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:A.从一个社区随机选取200名居民;B.从一个城镇的不同住宅楼中随机选取200名居民;C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市次项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:A.从一个社区随机选取200名居民;B.从一个城镇的不同住宅楼中随机选取200名居民;C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
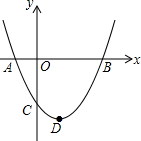 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com