
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
【答案】B
【解析】解:①由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故③正确;②∵二次函数y=ax2+bx+c开口向下,且对称轴为x= ![]() =1.5,∴当x≥1.5时,y的值随x值的增大而减小,故②错误;③∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故③正确;④∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故④正确.
=1.5,∴当x≥1.5时,y的值随x值的增大而减小,故②错误;③∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故③正确;④∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故④正确.
所以答案是:B.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c))的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
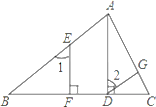
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
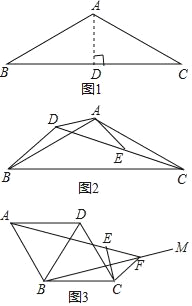
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,
∠BAC=60°,![]() .
.
(问题应用)
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,
(1)求证:△ADB≌△AEC;
(2)直接写出AD、BD、CD之间的数量关系;
如图3,菱形ABCD中,∠ABC=120°,在△ABC内部作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
(1)判断△EFC的形状,并给出证明.
(2)若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察)方程![]() 的解是
的解是![]() 的解是
的解是![]() ;
;
![]() 的解是
的解是![]() 的解是
的解是![]()
(发现)根据你的阅读回答问题:
(1)![]() 的解为_______;
的解为_______;
(2)关于![]() 的方程
的方程![]() 的解为_______(用含
的解为_______(用含![]() 的代数式表示),并利用“方程的解的概念”验证.
的代数式表示),并利用“方程的解的概念”验证.
(类比)
(3)关于![]() 的方程
的方程![]() 的解为_________(用含
的解为_________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
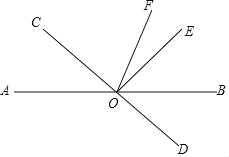
【题目】如图,直线AB,CD交于点O,OB平分∠DOE,OF是∠BOC的角平分线.
(1)说明:∠AOC=∠BOE;
(2)若∠AOC=46°,求∠EOF的度数;
(3)若∠EOF=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
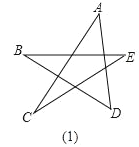
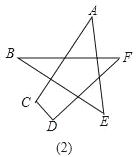
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
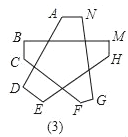
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD= ![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ![]() ,交OB于E点.
,交OB于E点.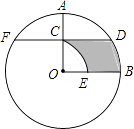
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
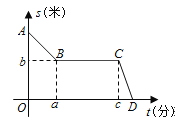
【题目】周老师为锻炼身体一直坚持步行上下班。已知学校到周老师家总路程为2000米,一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了20分钟,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值;
(2)b= ,c= .
(3)求周老师从学校到家的平均速度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com