

分析 (1)根据题意可以找到四张卡片中乘积最大的两张;
(2)根据题意可以找到四张卡片中相除乘积最小的两张;
(3)根据题意可以得到用运算符号连接结果为24的四张卡片,本题得以解决.
解答 解:(1)由题意可得,
从中抽出2张卡片,使这两张卡片上数字乘积最大,最大值是:(-5)×(-3)=15,
故答案为:15;
(2)由题意可得,
从中抽出2张卡片,使这两张卡片上数字相除的商最小,最小值是:(-5)÷3=$-\frac{5}{3}$,
故答案为:$-\frac{5}{3}$;
(3)由题意可得,
[(-3)-(-5)]×3×4=24,4×[3-(-3)]+0=24,[3-(-5)]×[0-(-3)]=24.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法,注意第三位答案不唯一,只要符号要求即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,一块正方形的铁皮,边长为x cm(x>4),如果一边截去宽4cm的一块,相邻一边截去宽3cm的一块.
如图,一块正方形的铁皮,边长为x cm(x>4),如果一边截去宽4cm的一块,相邻一边截去宽3cm的一块.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
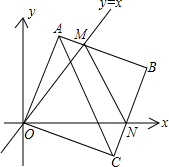 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com