若第一象限内的整点(n,m)位于抛物线y=19x2-98x上,则m+n的最小值为 .
【答案】
分析:由点(n,m)位于抛物线y=19x
2-98x上,代入y=19x
2-98x,进而得出m+n的关系式,分析得出答案即可.
解答:解:∵将(n,m)代入抛物线y=19x
2-98x,
m=19n
2-98n,
∴m+n=19n
2-98n+n,
=19n
2-97n,
=19n(n-

)>0,
∵5<
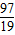
<6,n-

>0,又n为正整数
∴当n=6时,取得最小值,最小值为:m+n=19×36-97×6=102.
故答案为:102.
点评:此题主要考查了点在抛物线y=19x
2-98x上的特征,以及整数的特征,综合性较强.
