
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. 
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
【答案】
(1)证明:连接OE.
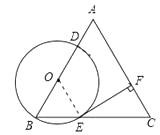
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°;
在△BOE中,OB=OE,∠B=60°,
∴∠B=∠OEB=∠BOE=60°,
∴∠BOE=∠A=60°,
∴OE∥AC(同位角相等,两直线平行);
∵EF⊥AC,
∴OE⊥EF,即直线EF是⊙O的切线
(2)解:连接DF.
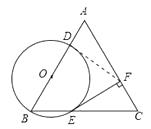
∵DF与⊙O相切,
∴∠ADF=90°.
设⊙O的半径是r,则EB=r,EC=4﹣r,AD=4﹣2r.
在Rt△ADF中,∠A=60°,
∴AF=2AD=8﹣4r.
∴FC=4r﹣4;
在Rt△CEF中,∵∠C=60°,∴EC=2FC,
∴4﹣r=2(4r﹣4),
解得,r= ![]() ;
;
∴⊙O的半径是 ![]() .
.
【解析】(1)连接OE.欲证直线EF是⊙O的切线,只需证明EF⊥AC.利用等边三角形的三个内角都是60°、等腰三角形OBE以及三角形的内角和定理求得同位角∠BOE=∠A=60°,从而判定OE∥AC,所以由已知条件EF⊥AC判定OE⊥EF,即直线EF是⊙O的切线;(2)连接DF.设⊙O的半径是r.由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于r的方程4﹣r=2(4r﹣4),解方程即可.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC= ![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC. 
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x>0),BC=y (y>0).求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F. 
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):﹣6,﹣3,x,2,﹣1,3,若这组数据的中位数是﹣1,在下列结论中:①方差是8;②极差是9;③众数是﹣1;④平均数是﹣1,其中正确的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( ) 
A.y= ![]() (x+3)2
(x+3)2
B.y= ![]() (x﹣3)2
(x﹣3)2
C.y=﹣ ![]() (x+3)2
(x+3)2
D.y=﹣ ![]() (x﹣3)2
(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() (x>0)的图像经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
(x>0)的图像经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB= ![]() ,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=
,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y= ![]() (x>0)的图像恰好经过DC的中点E.
(x>0)的图像恰好经过DC的中点E.
(1)求k的值和直线AE的函数表达式;
(2)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )
人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
金额(元) | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
A.极差是195000
B.中位数是15000
C.众数是15000
D.平均数是15000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com