
分析 (1)根据负整数指数幂、特殊角的三角函数值、零指数幂可以解答本题;
(2)先化简题目中的式子,然后将a的值代入即可解答本题.
解答 解:(1)(-$\frac{1}{3}$)-2-2cos45°+($\frac{π-3.14}{2}$)0+$\frac{1}{2}$$\sqrt{8}$+(-1)2017
=9-2×$\frac{\sqrt{2}}{2}$+1+$\frac{1}{2}×2\sqrt{2}$+(-1)
=$9-\sqrt{2}+1+\sqrt{2}-1$
=9;
(2)$\frac{a}{a-1}-\frac{3a-1}{{a}^{2}-1}$
=$\frac{a(a+1)}{{{a^2}-1}}-\frac{3a-1}{{{a^2}-1}}$
=$\frac{{{a^2}-2a+1}}{{{a^2}-1}}$
=$\frac{(a-1)^{2}}{(a+1)(a-1)}$
=$\frac{a-1}{a+1}$,
当$a=\sqrt{2}-1$时,原式=$\frac{\sqrt{2}-1-1}{\sqrt{2}-1+1}$=$\frac{{\sqrt{2}-2}}{{\sqrt{2}}}$=1$-\sqrt{2}$.
点评 本题考查分式的化简求值、实数的运算、负整数指数幂、特殊角的三角函数值、零指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是(0,3)、(4,0)、($\frac{7}{4}$,0).
如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是(0,3)、(4,0)、($\frac{7}{4}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
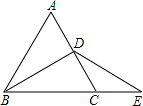 如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.
如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
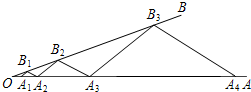 如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.
如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com