
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
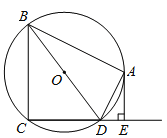
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
【答案】
【1】 证明:边结OA,
∵OA=OD,∴∠1=∠2.
∵DA平分![]() ,∴∠2=∠3.
,∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,[
∵![]() ,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,∴AE是⊙O的切线.
【2】 ∵BD是⊙O的直径,∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.∴![]()
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,得BD=![]() .
.
∴⊙O半径为![]() .
.
【解析】
试题(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长.
试题解析:(1)连接OA,
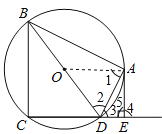
∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,
∵AE⊥CD,∴∠4=90°.
∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线.
(2)∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.
∴![]() ,
,
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,
得BD=![]() .
.
∴⊙O半径为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
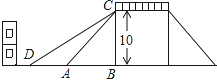
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点![]() 与点
与点![]() 之间的距的距离为
之间的距的距离为![]() 个单位长度,点
个单位长度,点![]() 在原点的左侧,到原点的距离为
在原点的左侧,到原点的距离为![]() 个单位长度,点
个单位长度,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 表示的数与点
表示的数与点![]() 表示的数互为相反数,动点
表示的数互为相反数,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,设移动时间为
移动,设移动时间为![]() 秒.
秒.
(1)点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 .
表示的数为 .
(2)用含![]() 的代数式分别表示点
的代数式分别表示点![]() 到点
到点![]() 和点
和点![]() 的距离:
的距离:![]() ,
,![]() .
.
(3)当点![]() 运动到
运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 点运动,点
点运动,点![]() 到达
到达![]() 点后,立即以同样的速度返回点
点后,立即以同样的速度返回点![]() ,在点
,在点![]() 开始运动后,当
开始运动后,当![]() 两点之间的距离为
两点之间的距离为![]() 个单位长度时,求此时点
个单位长度时,求此时点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示
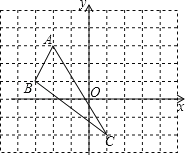
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学有一本零钱记账本,上面记载着某一周初始零钱为100元,周一到周五的收支情况如下(记收入为+,单位:元):
+25,-15.5,-23,-17,+26
(1)这周末他可以支配的零钱为几元?
(2)若他周六用了![]() 元购得2本书,周日他爸爸给了他10元买早饭,但他实际用了15元,恰好用完了所有的零钱,求
元购得2本书,周日他爸爸给了他10元买早饭,但他实际用了15元,恰好用完了所有的零钱,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
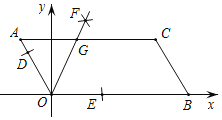
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com