
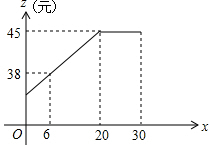
 大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.
大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.分析 (1)根据图象得出销售价格z与销售时间x(天)的关系为一次函数关系进而求出即可;
(2)根据当1≤x≤20时,以及当20<x≤30时,表示出日销售利润,进而解答即可;
(3)首先利用(2)中所求解析式,利用二次函数的最值求法以及一次函数的增减性,得出9月份日销售利润最大为1225元,再利用已知列出等式方程45(1-a%)•20(1+6a%)-20×20(1+6a%)=1225-569,进而求出a的值即可.
解答 解:(1)由图象知,当1≤x≤20时,设z=kx+b,
则有:
$\left\{\begin{array}{l}{38=6k+b}\\{45=20k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=35}\end{array}\right.$,
即z=0.5x+35,
当20<x≤30时z=45.
综上:z=$\left\{\begin{array}{l}{\frac{1}{2}x+35(1≤x≤20)}\\{45(<x≤30}\end{array}\right.$;
(2)当1≤x≤20时,
W=yz-20y=(-2x+80)(0.5x+35)-20(-2x+80)=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)=-50x+2000,
即在9月1日这一天的日销售利润最大,为1100元;
(3)9月30日的价格为45元,日销售量为20个,
9月份当1≤x≤20时日销售利润为:
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225,
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元,
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)•20(1+6a%)-20×20(1+6a%)=1225-569,
(1+6a%)[900(1-a%)-400]=656,
(1+6a%)(900-9a-400)=656,
(1+6a%)(500-9a)=656,
500-9a+30a-54a2%=656,
方程两边同乘以100得:
54a2-2100a+15600=0,
化简得9a2-350a+2600=0,
a1=10,a2=$\frac{260}{9}$(舍).
答:a的值为10
点评 此题主要考查了二次函数与一次函数的应用和一元二次方程的应用,根据已知得出利润与销量之间的函数关系式是解题关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
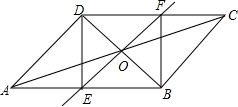 如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.
如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
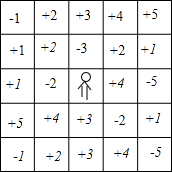 如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.
如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
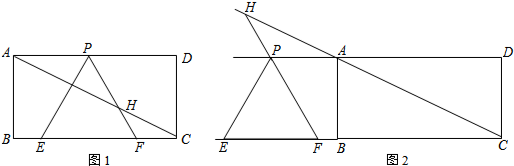
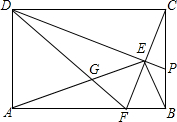 如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com