
 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题:分析 (1)根据图中条件即可得到结论;
(2)根据已知条件得到(a+b)2=a2+b2+2ab=81,于是得到结论;
(3)设5+2x=a,2x+3=b,则a2+b2=60,a-b=2,于是得到结论.
解答 解:(1)根据图中条件得,a2+b2+2ab=(a+b)2;
(2)∵a2+b2=57,ab=12,
∴(a+b)2=a2+b2+2ab=81,
∵a+b>0,
∴a+b=9;
(3)设5+2x=a,2x+3=b,
则a2+b2=60,a-b=2,
∵a2+b2-2ab=(a-b)2,
∴60-2ab=4,∴ab=28,
∴(5+2x)(2x+3)=28.
点评 本题考查对完全平方公式几何意义的理解与运用,应从整体和部分两方面来理解完全平方公式的几何意义.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
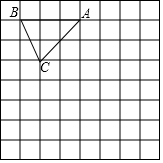 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
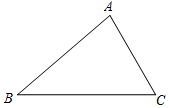 已知△ABC,请按要求完成画图、说明画图过程及画图依据.
已知△ABC,请按要求完成画图、说明画图过程及画图依据.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
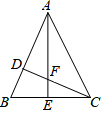 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若S△ABC=12,△ADF的面积为S1,△CFE的面积为S2,则S1-S2=2.
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若S△ABC=12,△ADF的面积为S1,△CFE的面积为S2,则S1-S2=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com