
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=AC=6cmЃЌЁЯB=ЁЯCЃЌBC=4cmЃЌЕуDЮЊABЕФжаЕуЃЎ
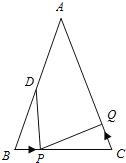
ЃЈ1ЃЉШчЙћЕуPдкЯпЖЮBCЩЯвд1cm/sЕФЫйЖШгЩЕуBЯђЕуCдЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮCAЩЯгЩЕуCЯђЕуAдЫЖЏЃЎ
ЂйШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌОЙ§1УыКѓЃЌЁїBPDгыЁїCQPЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЂкШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌЕБЕуQЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙЁїBPDгыЁїCQPШЋЕШЃП
ЃЈ2ЃЉШєЕуQвдЂкжаЕФдЫЖЏЫйЖШДгЕуCГіЗЂЃЌЕуPвддРДЕФдЫЖЏЫйЖШДгЕуBЭЌЪБГіЗЂЃЌЖМФцЪБеыбиЁїABCШ§БпдЫЖЏЃЌдђОЙ§ КѓЃЌЕуPгыЕуQЕквЛДЮдкЁїABCЕФ БпЩЯЯргіЃПЃЈдкКсЯпЩЯжБНгаДГіД№АИЃЌВЛБиЪщаДНтЬтЙ§ГЬЃЉ
ЁОД№АИЁПЃЈ1ЃЉЂйШЋЕШЃЌРэгЩМћНтЮіЃЛЂк1.5cm/sЃЛЃЈ2ЃЉ24УыЃЌAC.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОнЪБМфКЭЫйЖШЗжБ№ЧѓЕУСНИіШ§НЧаЮжаBPЁЂCQКЭBDЁЂPCБпЕФГЄЃЌИљОнSASХаЖЈСНИіШ§НЧаЮШЋЕШЃЎ
ЂкИљОнШЋЕШШ§НЧаЮгІТњзуЕФЬѕМўЬНЧѓБпжЎМфЕФЙиЯЕЃЌдйИљОнТЗГЬ=ЫйЖШЁСЪБМфЙЋЪНЃЌЯШЧѓЕУЕуPдЫЖЏЕФЪБМфЃЌдйЧѓЕУЕуQЕФдЫЖЏЫйЖШЃЛ
ЃЈ2ЃЉИљОнЬтвтНсКЯЭМаЮЗжЮіЗЂЯжЃКгЩгкЕуQЕФЫйЖШПьЃЌЧвдкЕуPЕФЧАБпЃЌЫљвдвЊЯыЕквЛДЮЯргіЃЌдђгІИУБШЕуPЖрзпЕШбќШ§НЧаЮЕФСНИіБпГЄЃЎ
НтЃКЃЈ1ЃЉЂйШЋЕШЃЌРэгЩШчЯТЃК
Ёпt=1УыЃЌ
ЁрBP=CQ=1ЁС1=1РхУзЃЌ
ЁпAB=6cmЃЌЕуDЮЊABЕФжаЕуЃЌ
ЁрBD=3cmЃЎ
гжЁпPC=BCЉBPЃЌBC=4cmЃЌ
ЁрPC=4Љ1=3cmЃЌ
ЁрPC=BDЃЎ
гжЁпAB=ACЃЌ
ЁрЁЯB=ЁЯCЃЌ
ЁрЁїBPDЁеЁїCQPЃЛ
ЂкМйЩшЁїBPDЁеЁїCQPЃЌ
ЁпvPЁйvQЃЌ
ЁрBPЁйCQЃЌ
гжЁпЁїBPDЁеЁїCQPЃЌЁЯB=ЁЯCЃЌдђBP=CP=2ЃЌBD=CQ=3ЃЌ
ЁрЕуPЃЌЕуQдЫЖЏЕФЪБМфt=![]() =2УыЃЌ
=2УыЃЌ
ЁрvQ=![]() =
=![]() =1.5cm/sЃЛ
=1.5cm/sЃЛ
ЃЈ2ЃЉЩшОЙ§xУыКѓЕуPгыЕуQЕквЛДЮЯргіЃЌ
гЩЬтвтЃЌЕУ 1.5x=x+2ЁС6ЃЌ
НтЕУx=24ЃЌ
ЁрЕуPЙВдЫЖЏСЫ24sЁС1cm/s=24cmЃЎ
Ёп24=2ЁС12ЃЌ
ЁрЕуPЁЂЕуQдкACБпЩЯЯргіЃЌ
ЁрОЙ§24УыЕуPгыЕуQЕквЛДЮдкБпACЩЯЯргіЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШбќШ§НЧаЮЕФСНБпГЄЗжБ№ЮЊ4ЁЂ9ЃЌдђЫќЕФжмГЄЮЊЃЈ ЃЉ
AЃЎ22 BЃЎ17 CЃЎ17Лђ22 DЃЎ13
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє3x2a+by2гыЉ4x3y3aЉbЪЧЭЌРрЯюЃЌдђaЉbЕФжЕЪЧЃЈЁЁЁЁЃЉ
A. 0 B. 1 C. 2 D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛдЊЖўДЮЗНГЬx2Љ8xЉ1=0ХфЗНКѓПЩБфаЮЮЊЃЈ ЃЉ
AЃЎЃЈx+4ЃЉ2=17
BЃЎЃЈx+4ЃЉ2=15
CЃЎЃЈxЉ4ЃЉ2=17
DЃЎЃЈxЉ4ЃЉ2=15
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЭМаЮжаЃЌВЛвЛЖЈЪЧжсЖдГЦЭМаЮЕФЪЧ
A. ЯпЖЮ B. ЕШбќШ§НЧаЮ C. ЕШбќЬнаЮ D. ЦНааЫФБпаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌDЪЧABБпЩЯвЛЕуЃЌвдCDЮЊБпзїЕШБпЁїCDEЃЌЪЙЕуEЁЂAдкжБЯпDCЕФЭЌВрЃЌСЌНгAEЃЌХаЖЯAEгыBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЖрБпаЮЕФФкНЧКЭЪЧЭтНЧКЭЕФ3БЖЃЌдђетИіЖрБпаЮЕФБпЪ§ЮЊ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDЁЂEЗжБ№дкБпBCЁЂACЩЯЃЌСЌНгADЁЂDEЃЌЧвЁЯ1=ЁЯB=ЁЯCЃЎ
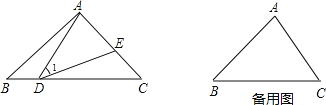
ЃЈ1ЃЉгЩЬтЩшЬѕМўЃЌЧыаДГіШ§Иіе§ШЗНсТлЃКЃЈвЊЧѓВЛдйЬэМгЦфЫћзжФИКЭИЈжњЯпЃЌевНсТлЙ§ГЬжаЬэМгЕФзжФИКЭИЈжњЯпВЛФмГіЯждкНсТлжаЃЌВЛБижЄУїЃЉ
Д№ЃКНсТлвЛЃК ЃЛ
НсТлЖўЃК ЃЛ
НсТлШ§ЃК ЃЎ
ЃЈ2ЃЉШєЁЯB=45ЁуЃЌBC=2ЃЌЕБЕуDдкBCЩЯдЫЖЏЪБЃЈЕуDВЛгыBЁЂCжиКЯЃЉЃЌ
ЂйЧѓCEЕФзюДѓжЕЃЛ
ЂкШєЁїADEЪЧЕШбќШ§НЧаЮЃЌЧѓДЫЪБBDЕФГЄЃЎ
ЃЈзЂвтЃКдкЕкЃЈ2ЃЉЕФЧѓНтЙ§ГЬжаЃЌШєгадЫгУЃЈ1ЃЉжаЕУГіЕФНсТлЃЌаыМгвджЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com