
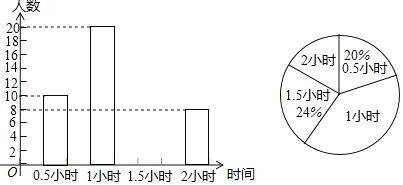
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)补全频数分布直方图;
(2)表示户外活动时间1小时的扇形圆心角的度数是多少;
(3)本次调查学生参加户外活动时间的众数是多少,中位数是多少;
(4)本次调查学生参加户外活动的平均时间是否符合要求?
【答案】(1)频数分布直方图如图所示;见解析;(2)在扇形统计图中的圆心角度数为144°;(3)1小时,1小时;(4)平均活动时间符合要求.
【解析】
(1)先根据条形统计图和扇形统计图的数据,由活动时间为0.5小时的数据求出参加活动的总人数,然后求出户外活动时间为1.5小时的人数;
(2)先根据户外活动时间为1小时的人数,求出其占总人数的百分比,然后算出其在扇形统计图中的圆心角度数;
(3)根据中位数和众数的概念,求解即可.
(4)根据平均时间=总时间÷总人数,求出平均时间与1小时进行比较,然后判断是否符合要求;
(1)调查总人数为:10÷20%=50(人),
户外活动时间为1.5小时的人数为:50×24%=12(人),
频数分布直方图如右图所示;
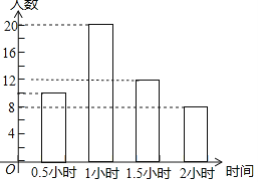
(2)户外活动时间为1小时的人数占总人数的百分比为:![]() ×100%=40%,
×100%=40%,
在扇形统计图中的圆心角度数为:40%×360°=144°.
(3)将50人的户外活动时间按照从小到大的顺序排列,
可知第25和第26人的户外运动时间都为1小时,故本次户外活动时间的中位数为1小时;
由频数分布直方图可知,户外活动时间为1小时的人数最多,故本次户外活动时间的众数为1小时.
(4)户外活动的平均时间为:![]() ×(10×0.5+20×1+12×1.5+8×2)=1.18(小时),
×(10×0.5+20×1+12×1.5+8×2)=1.18(小时),
∵1.18>1,
∴平均活动时间符合要求.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
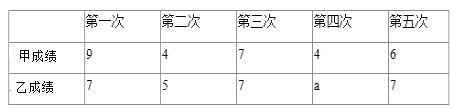
【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5剑,他们的总成绩![]() 单位:环
单位:环![]() 相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差
相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差![]() 见小宇的作业
见小宇的作业![]() .
.

![]() ______,
______,![]() ______;
______;
![]() 请完成图中乙成绩变化情况的折线;
请完成图中乙成绩变化情况的折线;
![]() 观察你补全的折线图可以看出______
观察你补全的折线图可以看出______![]() 填“甲”或“乙”
填“甲”或“乙”![]() 的成绩比较稳定
的成绩比较稳定![]() 参照小宇的计算方法,计算乙成绩的方差,并验证你的判断;并判断谁将被选中.
参照小宇的计算方法,计算乙成绩的方差,并验证你的判断;并判断谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你认真阅读材料,然后解答问题:
材料:在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”![]() .
.
例如:三点的坐标分别为![]() ,
,![]() ,
,![]() ,则“水平底”
,则“水平底”![]() ,“铅垂高”
,“铅垂高”![]() ,“矩面积”
,“矩面积”![]() .
.
问题:
![]() 若
若![]() ,
,![]() ,
,![]() ,“水平底”
,“水平底”![]() ______,“铅垂高”
______,“铅垂高”![]() ______,“矩面积”
______,“矩面积”![]() ______.
______.
![]() 若
若![]() ,
,![]() ,
,![]() 的矩面积为12,求P点的坐标.
的矩面积为12,求P点的坐标.
![]() 若
若![]() ,
,![]() ,
,![]() ,请直接写出A、B、P三点的“矩面积”的最小值.
,请直接写出A、B、P三点的“矩面积”的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划最多用41万元购买8台这两种型号的机器人,则该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
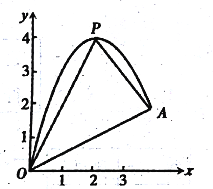
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知∠MAN=120°,AC平分∠MAN,∠ABC=∠ADC=90°,则能得到如下两个结论:①DC=BC;②AD+AB=AC. 请你证明结论②.
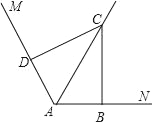
(2)如图,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
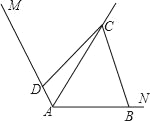
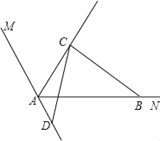
(3)如图3,如果D在AM的反向延长线上,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC=∠ADC,其他条件不变,(1)中的结论是否仍然成立?若成立,请直接回答;若不成立,你又能得出什么结论,直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 互补.
互补.
(1)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)如图![]() ,
,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() ;
;
(3)如图![]() ,在(2)的条件下,连接
,在(2)的条件下,连接![]() ,
,![]() 是
是![]() 上一点使
上一点使![]() ,作
,作![]() 平分
平分![]() ,问
,问![]() 的大小是否发生变化?若不变,请求出求值;若变化,说明理由.
的大小是否发生变化?若不变,请求出求值;若变化,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com