

分析 (1)根据平行线的性质和角平分线的性质求出∠PAQ+∠PCQ=90°,再根据三角形的内角和即可得出∠Q的度数;
(2)先延长AP交CD于点E,延长AQ交CD于点F,根据平行线的性质得出∠BAQ=∠CFQ,∠PEC=∠BAE,根据三角形的外角得出∠APC=∠PCE+∠PEC=∠PCE+∠BAE=2∠QCF+2∠BAE=2(∠QCF+∠BAE),最后根据∠AQC=∠QCF+∠BAE即可得出∠APC=2∠AQC.
(3)连接RQ,并延长RQ,连接RP并延长RP,利用三角形的外角得出∠AQC=∠ARC+∠QCR+∠QAR,从而得出2∠AQC=2∠ARC+2∠QCR+2∠QAR ①,根据∠APC=∠ARC+2∠QAR+2∠QCR ②,由①-②即可得出2∠AQC-∠APC=∠ARC.
解答 解:(1)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AQ、CQ是∠PAB和∠PCD的平分线,
∴∠Q=90°;
(2)延长AP交CD于点E,延长AQ交CD于点F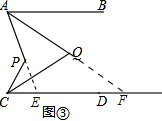
∵AB∥CD,
∴∠BAQ=∠CFQ,∠PEC=∠BAE,
∴∠APC=∠PCE+∠PEC=∠PCE+∠BAE=2∠QCF+2∠BAE=2(∠QCF+∠BAE),
∵∠AQC=∠QCF+∠BAE,
∴∠APC=2∠AQC.
(3)连接RQ,并延长RQ,
连接RP并延长RP,
∵∠AQC=∠3+∠4,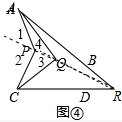
∴∠AQC=∠QRC+∠QCR+∠QAR+∠QRA=∠ARC+∠QCR+∠QAR,
∴2∠AQC=2∠ARC+2∠QCR+2∠QAR ①,
∵∠APC=∠1+∠2,
∴∠APC=2∠QAR+∠ARP+2∠QCR+∠CRP=∠ARC+2∠QAR+2∠QCR ②,
∴①-②得,
2∠AQC-∠APC=∠ARC.
点评 此题考查了平行线的性质,用到的知识点是平行线的性质、三角形的外角、三角形的内角和定理,关键是根据题意画出图形作出辅助线.


科目:初中数学 来源: 题型:解答题
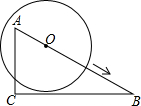 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
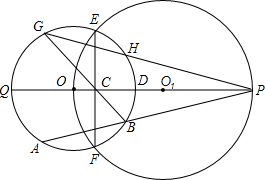 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
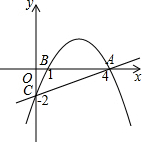 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com