
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )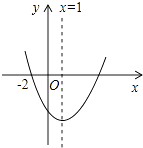
A.5
B.4
C.3
D.2
【答案】B
【解析】解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣ ![]() =1,
=1,
∴b=﹣2a<0,
而抛物线与y轴的交点在x轴下方,
∴c<0,
∴bc>0,所以①正确;
∵b=﹣2a,
∴b+2a=0,所以②正确;
∵x=﹣1时,y<0,
∴a﹣b+c<0,即a+c<b,所以③错误;
∵二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),且对称轴为直线x=1,
∴二次函数y=ax2+bx+c(a≠0)的图象过(4,0),
即x=4时,y=0,
∴16a+4b+c=0,所以④正确;
∵a﹣b+c<0,b=﹣2a,
∴a+2a+c<0,即3a+c<0,所以⑤正确.
所以答案是:B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
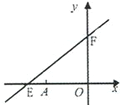
【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
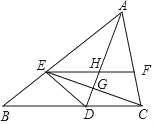
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
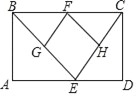
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图: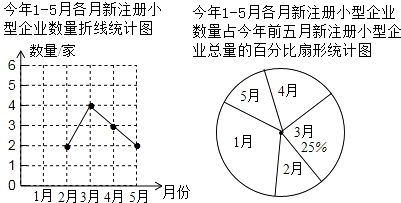
(1)某镇今年1﹣5月新注册小型企业一共有家.请将折线统计图补充完整;
(2)该镇今年4月新注册的小型企业中,只有2家是餐饮企业,现从4月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.

(1)求证:△AEB≌△CDA;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2________180°. ∵l1∥l2,∴∠1________∠3. ∵∠1+∠2 _______180°,∴∠3+∠2≠180°,这和________矛盾,∴假设∠1+∠2__________180°不成立,即∠1+∠2=180°.
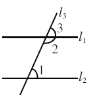
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com