
【题目】甲,乙两人以相同路线前往距离单位10![]() 的培训中心参加学习.图中
的培训中心参加学习.图中![]() 分别表示甲,乙两人前往目的地所走的路程s
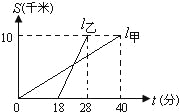
分别表示甲,乙两人前往目的地所走的路程s![]() 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8![]() 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
试题此题考查的是读函数的图象,首先要理解横纵坐标表示的含义,函数的横坐标表示时间,纵坐标表示路程,理解问题叙述的过程,能够通过图象知道函数是随自变量的增大而增大,然后根据图象上特殊点的意义进行解答:
①乙在28分时到达,甲在40分时到达,所以乙比甲提前了12分钟到达;故①正确;
②根据甲到达目的地时的路程和时间知:甲的平均速度=10÷4060=15千米/时;
③设乙出发x分钟后追上甲,则有:102818×x=1040×(18+x),解得x=6,乙第一次遇到甲时,所走的距离为:6×102818=6km,故③错误;
④由③得知正确.
因此正确的结论有三个:①②④.故选:B


科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A. 17cm B. 7cm C. 12cm D. 17cm或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案:______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.
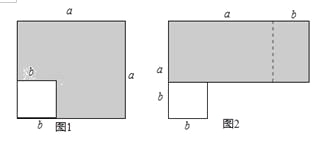
(1)如图1,阴影部分的面积是: ;
(2)如图2,是把图1重新剪拼成的一个长方形,阴影部分的面积是 ;
(3)比较两阴影部分面积,可以得到一个公式是 ;
(4)运用你所得到的公式,计算:99.8×100.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB.CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
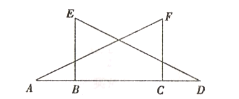
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
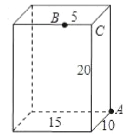
【题目】如图,长方形的长为15,宽为10,高为20,点![]() 离点
离点![]() 的距离为5,蚂蚁如果要沿着长方形的表面从点
的距离为5,蚂蚁如果要沿着长方形的表面从点![]() 爬到点
爬到点![]() ,需要爬行的最短距离是( )
,需要爬行的最短距离是( )
A.35B.![]() C.25D.
C.25D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com