
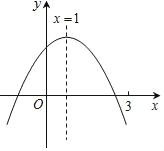
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②3a+c<0;③a+b≥am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.
其中正确的有( )个.
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
由抛物线开口方向得到a<0,利用抛物线的对称轴方程得到b=-2a>0,由抛物线与x轴的交点位置得到c>0,则可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)与(0,0)之间,所以当x=-1时,a-b+c<0,则可对④进行判断;把b=-2a代入可对②进行判断;利用二次函数的最值问题对③进行判断;把ax12+bx1=ax22+bx2进行变形得到(x1-x2)[a(x1+x2)+b]=0,从而得到a(x1+x2)+b=0,再利用b=-2a可对⑤进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b=-2a>0,
∵抛物线与x轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线与x轴的一个交点在(2,0)与(3,0)之间,
∴抛物线与x轴的另一个交点在(-1,0)与(0,0)之间,
∴当x=-1时,y<0,
即a-b+c<0,所以④错误;
∴a+2a+c<0,即3a+c<0,所以②正确;
∵x=1时,y有最大值,
∴a+b+c≥am2+bm+c,
即a+b≥am2+bm,所以③正确;
∵ax12+bx1=ax22+bx2,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,
∴x1+x2=-![]() =-
=-![]() =2,所以⑤正确.
=2,所以⑤正确.
故选B.


科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
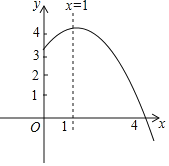
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.

已知:如图,钝角∠AOB.求作:∠AOB的角平分线.
作法:
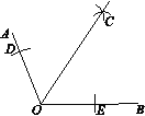
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() 的长为半径作弧,在∠AOB内,两弧交于点C;
的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程:
由①可得:OD=OE
由②可得:_________________
由③可知:OC=OC
∴______≌_________(依据:________________________)
∴可得∠COD=∠COE(全等三角形对应角相等)
即OC就是所求作的∠AOB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
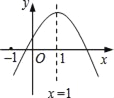
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com