
【题目】某学校八年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置—、二、三等奖和进步奖共四个奖项,赛后将八年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请报据图中的信息,解答下列问题:

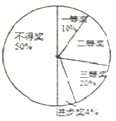
(1)八年级(1)班共有 名学生;
(2)将条形图补充完整;在扇形统计图中,“二等奖”对应的扇形的圆心角度数 ;
(3)如果该八年级共有800名学生,请估计荣获一、二、三等奖的学生共有多少名.
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() 时,给出以下结论:①
时,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长的最小值是
的周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
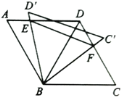
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市某种出租车收费标准如下:乘车里程不超过3公里的一律收费10元,乘车里程超过3公里的,超过部分按每公里1.8元加收.
(1)如果有人乘该出租车行驶了8公里,那么他应付多少车费?
(2)如果该人行驶了x(x>3)公里,他应付多少车费?
(3)某游客乘出租车从A地到B地,付车费22.6元,试估算从A地到B地大约多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况.
指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况. ![]() 的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市
的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市![]() 年与
年与![]() 年
年![]() 涨跌率的统计图中的信息,请判断
涨跌率的统计图中的信息,请判断![]() 年
年![]() ~
~![]() 月份与
月份与![]() 年
年![]() ~
~![]() 月份,同月份比较
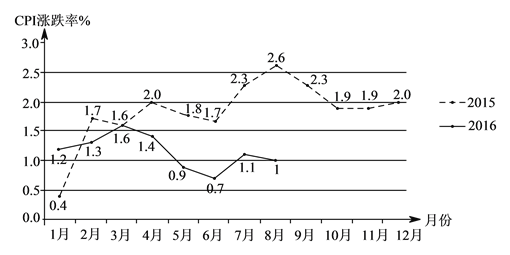
月份,同月份比较![]() 涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市
涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市![]() 年第四季度
年第四季度![]() 涨跌率变化趋势是__________,你的预估理由是__________;
涨跌率变化趋势是__________,你的预估理由是__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】准备两张同样大小的正方形纸片.
(1)取准备好的一张正方形纸片,将它的四周各剪去一个同样大小的正方形(如图1),再折合成一个无盖的长方体盒子.做成的长方体盒子的底面的边长为6cm,容积为108cm3,那么原正方形纸片的边长为多少?
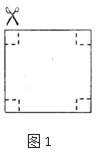
(2)取准备好的另一张一样的正方形纸片,这张纸片恰好可做成圆柱形食品罐侧面的包装纸(如图2,不计接口部分),求这个食品罐的底面圆的半径?(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多![]() 小时,求自行车的平均速度?
小时,求自行车的平均速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣5,0),B(1,0)两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.
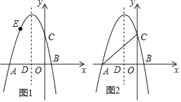
(1)求抛物线的函数表达式;
(2)如图1,点E(x,y)为抛物线上一点,且﹣5<x<﹣2,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,得到矩形EHDF,求矩形EHDF周长的最大值;
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,A,C为顶点的三角形是直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com