
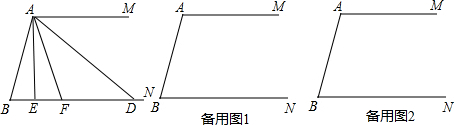
分析 (1)根据角平分线的定义可知“∠BAE=∠EAF=$\frac{1}{2}$∠BAF,∠FAD=∠DAM=$\frac{1}{2}$∠FAM”,结合角之间的关系即可得出∠EAD=$\frac{1}{2}$∠BAM,从而得出结论;
(2)根据平行线的性质结合∠EAD=∠B,可求出∠B和∠MAB的度数.按两种情况来考虑△AEF是直角三角形,通过角的计算可得出∠MAD的度数,结合平行线的性质即可得出结论.
解答 解:(1)∵AE平分∠BAF,AD平分∠MAF,
∴∠BAE=∠EAF=$\frac{1}{2}$∠BAF,∠FAD=∠DAM=$\frac{1}{2}$∠FAM,
∴∠EAD=∠EAF+∠FAD=$\frac{1}{2}$(∠BAF+∠FAM)=$\frac{1}{2}$∠BAM=$\frac{1}{2}$α.
(2)∵AM∥BN,
∴∠MAB+∠B=180°.
∵∠EAD=∠B=$\frac{1}{2}$∠MAB,
∴∠B=60°,∠MAB=120°.
△AEF是直角三角形分两种情况:
①∠AFE=90°.
∵∠B=60°,
∴∠BAF=90°-60°=30°,
∠MAF=∠MAB-∠BAF=90°.
∵AD平分∠MAF,
∴∠MAD=$\frac{1}{2}$∠MAF=45°.
∵AM∥BN,
∴∠ADB=∠MAD=45°;
②∠AEF=90°.
∵∠B=60°,∠MAB=120°,
∴∠BAE=90°-60°=30°,
∴∠BAF=2∠BAE=60°,
∠MAF=∠MAB-∠BAF=60°,
∵AD平分∠MAF,
∴∠MAD=$\frac{1}{2}$∠MAF=30°.
∵AM∥BN,
∴∠ADB=∠MAD=30°.
综上可知:在F点运动的过程中,如果△AEF恰好是直角三角形,此时∠ADB的度数为45°或30°.
点评 本题考查了平行线的性质、角平分线定义以及角的计算,解题的关键是:(1)根据角平分线的定义找出∠EAD=$\frac{1}{2}$∠BAM;(2)求出∠MAD的度数.本题属于基础题,难度不大,解决该题型题目时,合理的利用角的计算及平行线的性质定理是关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | -1+$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
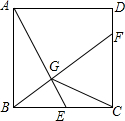 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.
如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2).
设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com